Hay frases que se quedan grabadas, bien por su repetición, o bien porque cuando las escuchas no se acaban de entender pero piensas que quieren decir algo. Esto sucede con las palabras del rey Salomón del libro de la Sabiduría [1]: «Tú lo ordenaste todo según el Número, el Peso y la Medida.»
Platón en el diálogo Filebo [2] insiste en la misma idea: “Si se apartan de todas las ciencias, las del Número, Peso y Medida, lo que quedara sería, por así decirlo, nulo”.
Son frases sintéticas que parecen expresar un gran contenido, pero ¿qué quieren decir?. El peso y la medida se expresan en números, por tanto la cuestión está en el Número.
Si buscamos en el Diccionario la palabra Número suele ser definida por la expresión “cantidad en relación a la unidad”, pero con esta definición no se abarca el número. Necesita de una in mensa cantidad de calificativos (ordinal, cardinal, entero, decimal, etc) para poder empezar a entender el concepto de Número.
Lo que sí sabemos es de su inmutabilidad porque son conceptos mentales. Cuando empezamos a hablar, comenzamos a enumerar, a generar…
San Agustín en el libro II de “El libre albedrío” [3] dice: «Contempla la hermosura de un cuerpo ya formado: están los números ocupando su lugar. Fíjate en la hermosura de un cuerpo que se mueve. Están los números obrando en el tiempo. Llégate al arte de donde éstos proceden y pregunta allí por el tiempo y el lugar, y no encontrarás ni tiempo ni espacio, sino que allí, en el arte, no hay más que números”.
Y cuando Platón en el diálogo Timeo [4] vuelve a insistir: “El tiempo imita a la eternidad y gira según el número”, parece que el conocimiento de nuestra cultura, ha elevado al Número a categoría de Ley que rige la creación del universo.
En esta creación todo está limitado. Todo comienza y todo concluye, hay un comienzo y un final. La mente a ese principio o comienzo le llama Uno. Hasta qué punto tenemos incorporado que todo tiene un final, hace que a la mente le resulte difícil comprender el concepto de infinito.
¿Qué es infinito? En principio, algo interminable, que no tiene fin en la misma dimensión. Pero infinito es también un cambio de dimensión. Para la línea es infinito el plano: éste contiene infinitas líneas; para el plano es inalcanzable el volumen: éste contiene infinitos planos,… Una palabra o sonido en la que la mente tiende a perder sus límites pareciendo diluirse en el vacío.
Pero la mente entiende perfectamente el nº 2 porque funciona por los pares de opuestos: blanco/negro, lleno/vacío, frío/calor, acción/reacción…. Al considerar los pares de opuestos, acota el problema y lo entiende. Es su forma de funcionar.
Pero éste proceso que la mente hace automáticamente es mucho más rico y complejo de lo que a primera vista pudiera parecer, porque entre el 1 y 2 están contenidos casi todos los elementos que dan origen a la teoría de la proporción.
Platón define la proporción con estas palabras [5]: “Es imposible combinar dos cosas sin la existencia de una tercera. Es preciso que haya un vínculo que las una. No hay mejor vínculo que el que hace de sí mismo y de las cosas que une, un todo único e idéntico”.
Y con esta definición nace el número 3 y el juego de la creación.
Vamos a empezar a hablar de proporciones básicas en la arquitectura desde el punto de vista geométrico. Euclides ya definía tres: la proporción aritmética, la geométrica y la armónica. En los tres casos, si de dos segmentos de diferente longitud A y B, queremos hallar sus medias, la primera operación es unirlos. Y qué mejor vínculo que la suma de ambos segmentos formen el diámetro de la circunferencia que les engloba.
La media aritmética corresponde al radio del círculo, la media geométrica al segmento vertical que corta al círculo en el punto de unión de ambos y la media armónica, aunque de construcción más compleja, queda definida a través del diámetro y la longitud de la circunferencia.
Palladio [6] las definía como medidas de habitación: así, si la planta es de 6mx12 m, la altura, como media aritmética es 9m. Si la planta mide 4mx9m, su altura, como media geométrica, es de 6m. Si por último, la planta mide 6mx12m su altura, como media armónica, es de 8m. Es decir, tres triadas numéricas: 6/9/12, 4/6/9 y 6/8/12.
Platón definía: la media aritmética como la “paridad del número”; la media geométrica como “la igualdad de cocientes” y de la media armónica, a la que consideraba más sutil, decía “ese número que es tanto mayor que el menor como es menor que el mayor”.
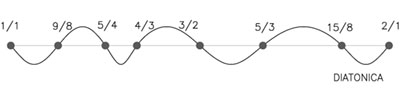
Si a estos segmentos les damos una longitud de 1 y 2, encontramos que le media aritmética es 3/2, ((a+b)/2), la media geométrica es √2 (√ab) la media armónica es 4/3 (2ab/(a+b)). Los valores 3/2 y 4/3 corresponden a los valores de las notas Quinta (Sol) y Cuarta (Fa) de la notación musical de la escala diatónica.
¿Qué valor tiene todo esto? Si hemos definido tres términos, podemos continuar… es decir, su valor es la capacidad de generar series que ordenan, proporcionalmente, los espacios. Por ejemplo, el sistema de numeración es una serie aritmética de razón 1. La serie aritmética que ya ha comenzado en 1, 3/2, 2 tiene su continuación en 5/2…. La serie geométrica 1, √2, 2 continua con 2, √2….
Hay series geométricas más sencillas, por ejemplo en base 2: 1, 2, 4, 8, 16… o lo que es lo mismo: 1, 21, 22, 23, 24,… o en base 3: 1, 3, 9, 27, 81… o lo que es lo mismo: 1, 31, 32, 33, …
Si tomamos los cuatro primeros números de estas dos serie geométricas, veremos surgir la Lambda de Platón en la que utiliza esta imagen para definir la creación del Alma del universo, y explica, en el diálogo Timeo, cómo esta estructura queda determinada por medias aritméticas y armónicas. Esta Lambda siempre se ha representado como un triángulo abierto en la base y las dos series apoyadas en los lados inclinados y con el interior vacío.
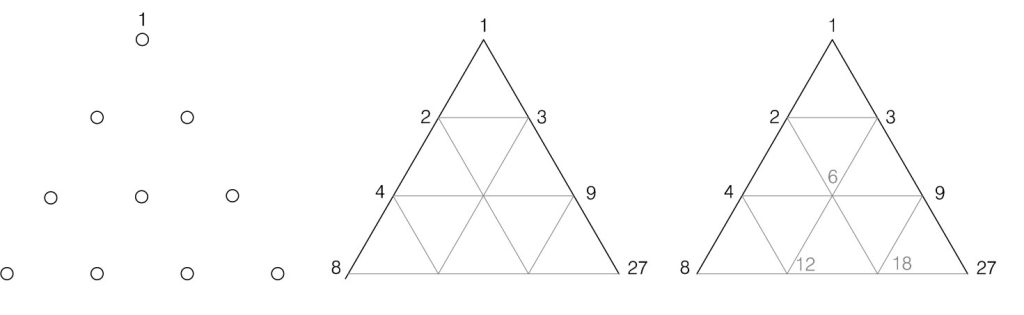
Este vacío puede ser rellenado por tres números. Números reconocibles de las triadas palladianas. Si se observa con detenimiento esta triple imagen que comienza con la Tetractys pitágorica, se evidencian las sencillas relaciones existentes entre estos diez primeros números.
Juan Borches [7] nos aporta algunos datos más. Dice que la antigüedad denominó “musical” a un tipo de relación de cuatro términos en los que se combinan las medias aritmética y armónica, la misma relación que Zarlino utilizó para establecer su gama a mediados del siglo XVI y que que tiene la siguiente notación algebraica:
a : (a+b / 2)= 2ab : (a+b) / b
donde reconocemos la M. aritméticva en el primer denom inador y la M. armónica en el segundo numerador, de lo que se deduce que el producto de dos segmentos o dimensiones es igual al producto de sus medias aritmética y armónica, esto traducido a números enteros es la conocida relación de cuarta, quinta y octava, 12:9=8:6, y que reflejaron geométricamente en una figura donde las longitudes correspondían a largos de cuerda. [8]
Con respecto a la media geométrica hace una aclaración interesante. Por ejemplo, si tenemos los dos segmentos 1 y 2, su media geométrica es √2; si lo traducimos a geometría, la media geométrica es un cuadrado de lado √2 y los segmentos de valores 1 y 2 son los lados de un rectángulo. Como el área del cuadrado es 2 y el área del rectángulo es 2, la media geométrica iguala superficies “por lo que la acción de esta media consiste en dividir el exceso entre los segmentos para que el área que engendran, quede igualmente repartida”. [9]
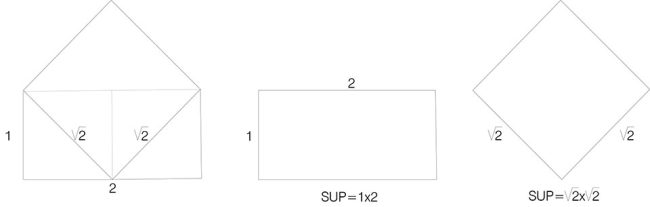
Estas descripciones geométricas y matemáticas de las medias, corresponden a un tipo de conocimiento “disciplinar”, y su posible utilización suele ser como una herramienta de control de las relaciones entre las dimensiones de un proyecto, pero parece que poco tienen que ver con la experiencia diaria. Pero el espacio lo vivimos en perspectiva y es, desde un punto concreto, donde observamos. Una forma de comprender que estas tres medias tienen una relación mucho más cercana al ser humano, es a través de una representación geométrica sencilla.
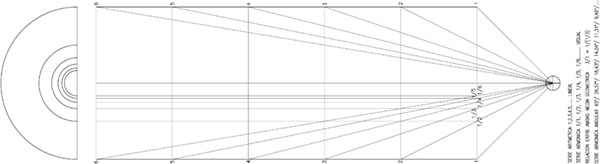
Consideremos que estamos contemplando un túnel situados en su eje en un punto determinado. Este túnel está construido con una serie de anillos estructurales colocados a la misma distancia. Desde nuestro punto de vista, veremos estos anillos como una serie de círculos concéntricos haciéndose cada vez más pequeños según se alejan.
Si las separaciones entre los anillos las planteamos como simples unidades, tendremos la serie aritmética 1, 2, 3, 4, 5, …. Si nosotros estamos colocados en el eje del túnel a esa misma distancia del comienzo, los radios de los círculos concéntricos que vemos en perspectiva serán: 1/1, 1/2, 1/3, 1/4, 1/5,…. que define una serie armónica.
Esto es, nuestra visión en perspectiva “ha traducido” la serie aritmética que define la situación de los anillos, en una serie armónica. O dicho de otra manera: nuestra percepción “ha traducido” el orden del plano al espacio.
Podríamos generalizar diciendo que el observador convierte las series aritméticas de la creación en series armónicas en su experiencia…
Notas:
Este artículo, el primero de una serie, corresponde a las clases teóricas sobre proporción, impartidas durante once años en la asignatura de Proyectos 2. Departamento de Arquitectura. Universidad Alfonso X El Sabio. Villanueva de la Cañada. Madrid
[1] Libro de la Sabiduría.Salomón. Sagrada Biblia. Biblioteca de Autores Cristianos. Madrid 1967
[2] Diálogos:Filebo. Platón. Ed. Ibérica.Juan B. Bergua. 1968
[3] El libre Albedrío. San Agustín. Obras Completas.Biblioteca de Autores Cristianos. Madrid 1976.
[4] Diálogo Timeo. Platón. Biblioteca Clásica Gredos. 1992
[5] Idem anterior.
[6] Palladio. Loa cuatro libros de arquitectura.
[7] Juan Borchers. Meta-arquitectura. Mathesis Ediciones. Santiago de Chile.1975. pg 97
[8] “La medición como sustrato del fenómeno arquitectural” Revista Hogar y Arquitectura nº 87. Marzo – Abril 1970
[9] Juan Borchers. Meta-Arquitectura. Idem anterior. pg.98
(Revisado: Agosto 2023)
» Publicaciones relacionadas: Proporción 2, Proporción 3, Proporción 4


Dejar un comentario