1.- INTRODUCCIÓN.
Los dos artículos anteriorescorrespondientes al nº φ y al nº ψ ya han desarrollado los aspectos que planteábamos en Parte 1 de esta serie dedicada a las Espirales de los nº geométricos. En ambos casos, se han considerado sus ciclos completos.
Ahora entramos en los dos números inconmensurables clásicos √2 y √3. √2 o diagonal del cuadrado de lado unidad y √3 o altura del triángulo equilátero de lado dos. Ambos tienen los ciclos más largos y por ello, las velocidades más lentas. Así, √2 necesita de 360 puntos para completar su recorrido mientras que √3 necesita de 720 puntos, o lo que es lo mismo √2 con movimientos angulares de 1º y √3 con 0,5º.
Dados sus largos ciclos, presentan la dificultad de su representación en este formato, por ello centraremos el estudio en los noventa primeros puntos de su recorrido; esto permite intuir las po-sibilidades contenidas en su desarrollo además de relacionarlos con los dos anteriores números geométricos. En ambos casos, se mantiene la misma razón lineal de crecimiento 49/48 que se ha aplicado al nº φ.
Empezamos con √2 recordando su crecimiento angular mediante giros de 149º [(360º x 1,4142= 509,11º) (509º-360º=149º)], el nº de vueltas, 149, y el nº de puntos, 360, necesarios para completar el ciclo de 360º.
La F1 (que corresponde a la F2 de Parte 1) contiene los 360 puntos del ciclo con una razón de crecimiento lineal de 81/80. El propio dibujo ya indica que la escala necesaria para su estudio está fuera de los límites de este formato y por ello, como ya hemos indicado nos centramos en los noventa primeros puntos.

Por qué 90 puntos? En el movimiento angular de este número el punto 90 define los 90º del ciclo. La nota Do o Unísono corresponde al punto 0 (0º), la nota Mi corresponde al punto 90 (90º) y la nota Octava al punto 360 (360º). Este dato aunque sea someramente, permite considerar la octava de 1/4, Do-Mi (0º/90º) ya desarrollada en los anteriores artículos. F2

Al igual que en las espirales del nº φ, se produce una distribución de los puntos en el espacio o plano, que la sola contemplación del dibujo, ya da indicios de las posibilidades contenidas hasta el punto de que el parecido con la distribución del nº φ, hace dudar de si es el mismo dibujo. Una mirada atenta de la situación del punto 1 en ambos dibujos con una diferencia angular de 11,5º, permite dilucidar la duda que se presenta.
2.- ESPIRALES DE √2.
Empezamos presentando las distintas espirales. Y así como en las anteriores espirales del nº Φ y del nº Ψ hemos seguido su crecimiento basado en la serie Fibonacci y en la serie de Padovan, en este caso, no ha habido decisión a priori sino que ha sido el propio examen y claridad de la organización de los puntos del nº √2, lo que ha decidido la selección de razones para el dibujo de estos primeros 90 puntos.
Así, en las F3, F4, F5, F6, F7, F8 y F9, están representadas las siguientes espirales:
– la razón 1/2 define 2 espirales levógiras.
– la razón 1/3 presenta 3 espirales dextrógiras.
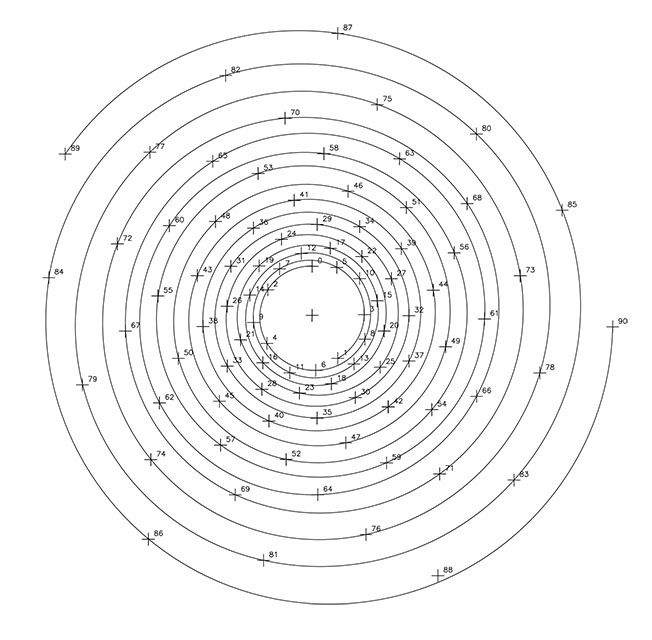
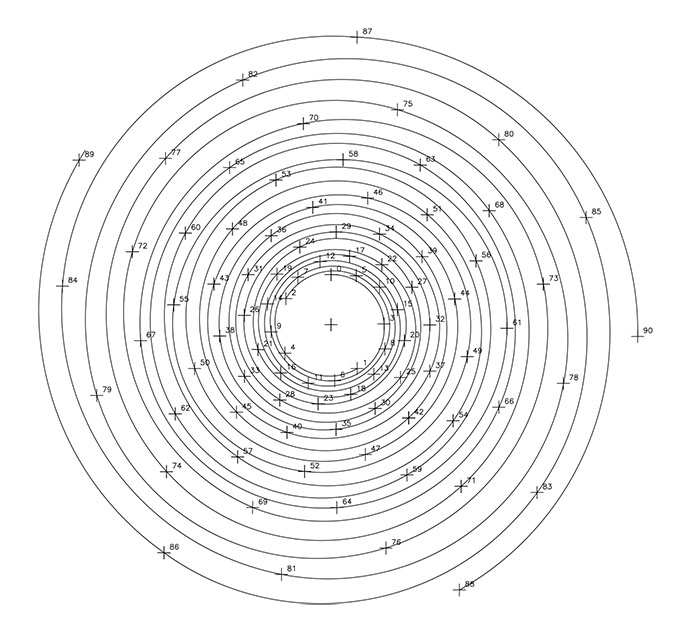
– la razón 1/5, 5 espirales dextrógiras.
– la razón 1/7, 7 espirales levógiras.
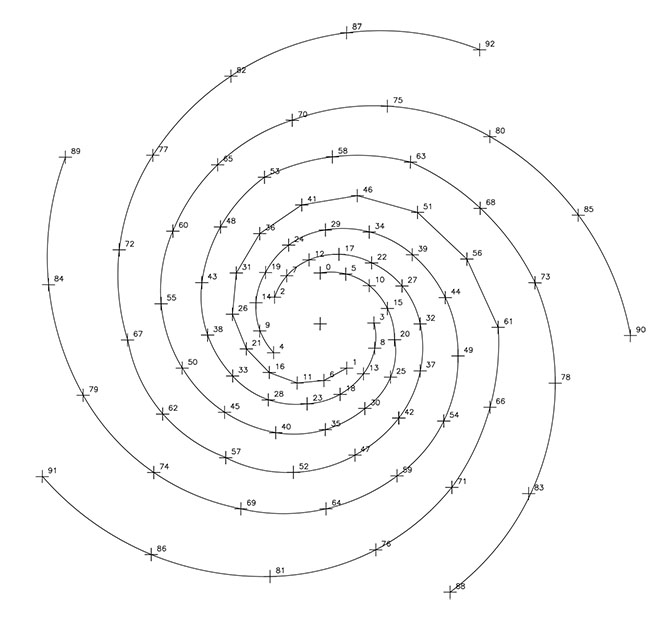
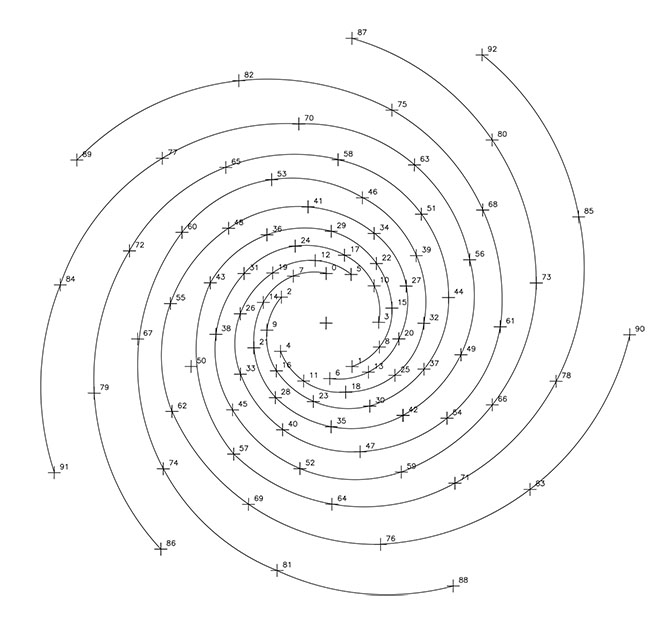
– la razón 1/12, 12 espirales levógiras.
– la razón 1/17, 17 espirales dextrógiras.
– la razón 1/29, 29 espirales dextrógiras.
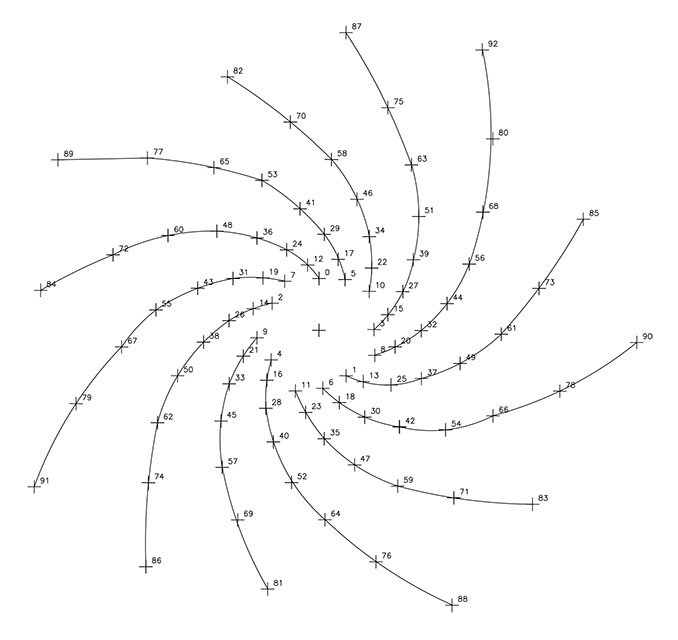
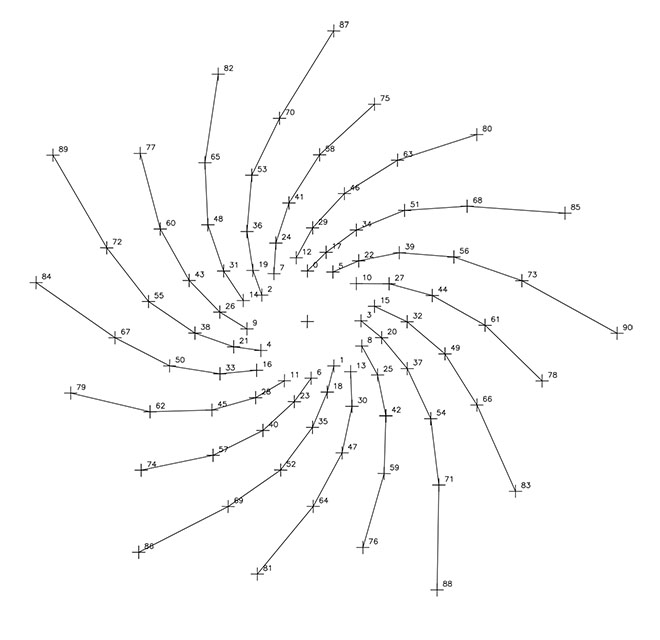
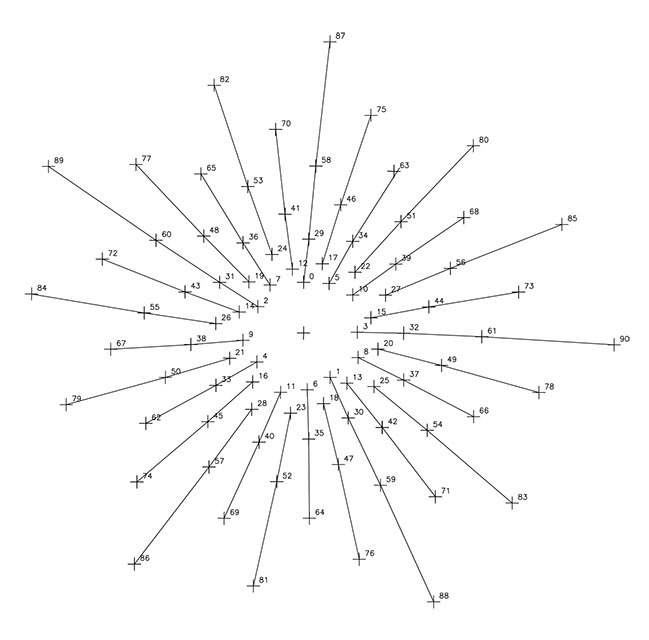
Al igual que en los anteriores artículos, la reducción de los puntos a los nueve primeros números reproduce la misma secuencia numérica. Así, la espiral 1/2 reproduce 2 espirales con el ritmo basado en los cinco primeros impares seguidos de los 4 pares alternando; la espiral 1/3 re-produce tres espirales dextrógiras guiadas por la triada 1/4/7, una segunda de ritmo 2/5/8 y una tercera guiada por 3/6/9, y así sucesivamente puesto que, recordemos, el ritmo viene indicado por el nº de saltos y no es específico de cada número geométrico.
Y así, como en las espirales del nº Φ, hemos visto esas simetrías implícitas entre las razones de las series de Fibonacci y de Lucas, aquí intuitivamente podemos apreciar esas posibles simetrías entre por ejemplo, las espirales de razón 1/5 y 1/7 y las espirales de razón 1/12 y 1/7. F10 y F11.
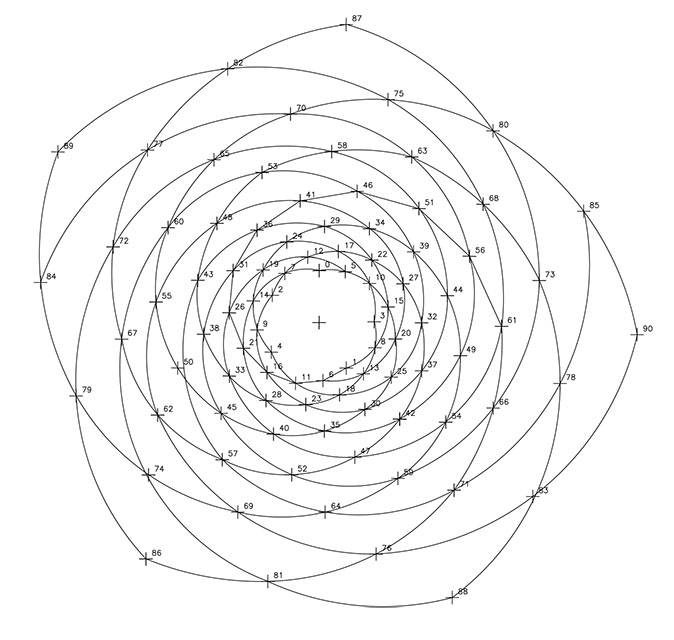
3.- VALOR DE LOS SECTORES.
De nuevo, recordemos que lo que hemos ido exponiendo se ha referido a las líneas o espirales que conectan los diferentes puntos de cada escenario espacial concreto.
Así, decíamos en Parte 2: «Formas lineales de gran belleza que al superponerse resultan en formas planares; planos cuya sectorización resulta de, al menos, dos espirales. Y así como hemos visto, ciclos y ritmos en las propias espirales, vamos a revisar qué sucede al estudiar el «valor» de esos sectores cuadrangulares cuyo dibujo recuerda la organización de los pétalos de las flores».
Esa reducción de la numeración a los nueve primeros números es un aspecto que facilita, por su claridad y sencillez, la comprensión y diferenciación de las características de esas formas planares. Ya lo hemos visto con el nº φ y ahora entramos en √2.
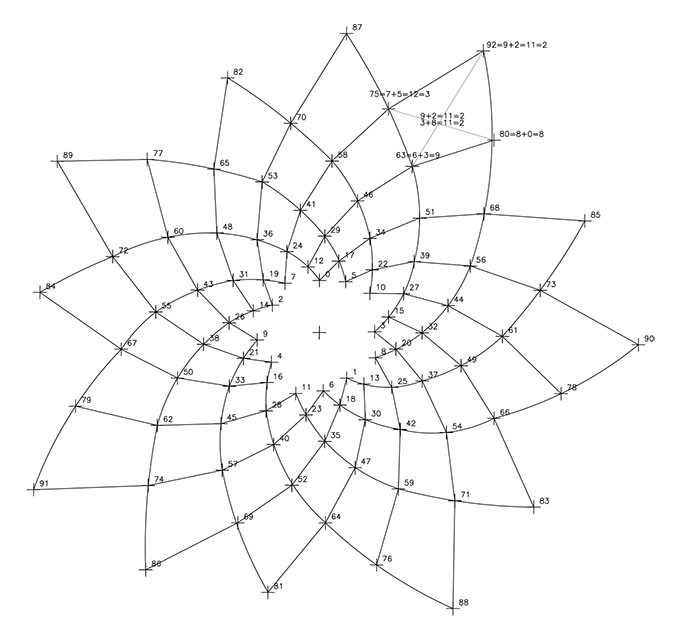
Vamos a hablar del «valor» de los sectores cuadrangulares que resultan de la superposición de dos espirales, la 1/12 y la 1/17 de la F12. Mediante esta figura se puede seguir el proceso.
Así por ejemplo, tomamos el sector cuadrangular definido por los vértices 92 (9+2=11=2), 63 (6+3=9), 80 (8+0=8), y 75 (7+5=12=3). Sumando los vértices opuestos diagonalmente tenemos 92+63=2 (2+9=11=2) y 80+75=2 (8+3=11=2). La igualdad de la suma remite al «valor» de 2 para este sector.
Tomemos el siguiente sector definido por los vértices 75 (7+5=12=3), 63 (6+3=9), 46 (4+6=10=1) y 58 (5+8=13=4). La unión de los vértices opuestos da 75+46= 4 (3+1=4) y 58+63=4 (4+9=13=4). El «valor» de este sector corresponde a 4.
Y si seguimos esa banda ancha dextrógira limitada por las dos espirales de razón 1/17 cuya serie son los números 12/29/46/63/80 y 7/24/41/58/75/92, «cortadas» por 5 de las espirales de razón 1/12, veremos que los sectores de dicha banda, desde el centro hacia fuera, siguen siempre el «valor» de los números pares: 8, 6, 4 y 2. A ambos lados, las bandas siguen los «valores» 7, 5, 3 y 1 (los números impares).
Con los mismos criterios, podemos seguir las bandas levógiras definidas por las espirales 1/12. Así, por ejemplo, la banda limitada por las dos espirales cuyas series son: 8/20/32/44/56/62/80/92 y 3/15/27/39/51/63/75/87, «cortadas» por siete de las espirales 1/17. Veremos que los sectores cuadrangulares resultantes toman un «valor», desde el centro hacia fuera, formado por la triada 8/5/2. A cada lado, le acompañan dos bandas, con dos nuevas triadas definidas por los «valores» de las triadas 1/4/7 y 3/6/9 en cada sector cuadrangular. Recordemos de nuevo, el dibujo del eneagrama y sus tres triadas.
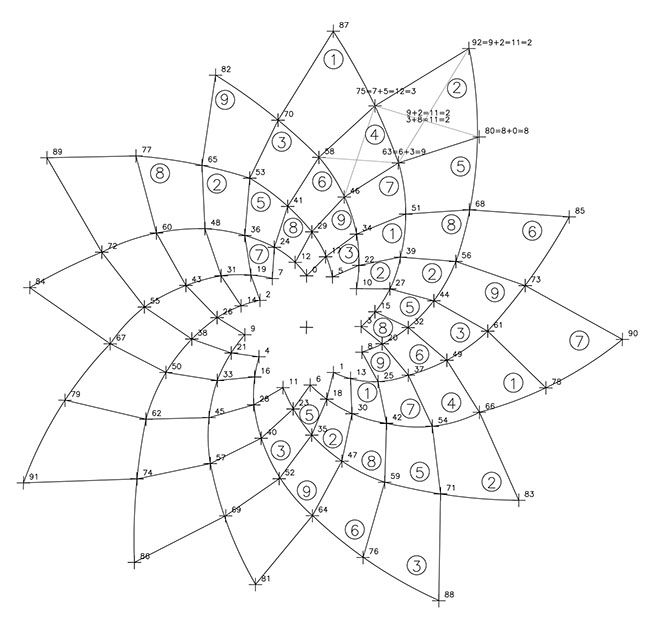
El resultado es una imagen con todos los sectores definidos por un «valor». F13.
Si observamos esta F13, veremos que todas las bandas definidas por las espirales 1/12 de sentido levógiro, van alternando el ritmo triádico (comenzando desde fuera hacia dentro) de los números 1/4/7, el 2/5/8 y el 3/6/9.
Si observamos las bandas definidas por la espirales de razón 1 /17 de sentido dextrógiro, veremos que comenzando de nuevo desde afuera hacia adentro, se va alternando el ritmo de los cuatro primeros números pares seguidos de los 5 impares y viceversa.
Una imagen sintética que expresa de manera sencilla los ritmos subyacentes que existen en estos procesos de expansión o crecimiento.
4.- ESPIRALES Y OCTAVA.
Así como hemos visto en las espirales del nº φ y del nº ψ su relación con la octava angular, igual vamos a ver su relación con el nº 2.(1)
En los 360 puntos del ciclo completo de √2, están contenidas las notas de la escala diatónica (1):
– Unisono y Octava en los p. 0 y 360.
– la nota Re corresponde al p. 225.
– la nota Mi está en el p.90.
– la nota Fa, corresponde al p. 240
– la nota Sol se sitúa en el p. 180.
– la nota La en el p.120.
– la nota Si en el p. 135.
Además aparecen:
– la relación 7/5 o Fa# como p. 216.
– la relación 8/5 o Sol # como p.144.
– la relación 7/4 o Sib como p. 270.
Dada la escala de representación en 90 puntos, el dibujo visible sólo admite la nota del Unísono o p.0 y la nota Mi o relación 5/4, como p.90 de la octava angular 1/1 (0º/360º). Aunque al igual que en las espirales anteriores, sí podemos situar algunas de las notas correspondientes a las octavas interiores de 1/8, Do/Re y Re/Mi (0º/45º) y de1/4, Do-Mi (0º/90º).
Si observamos la F14 veremos que, en la primera octava 1/8 Do-Re (0º/45º), aparecen las notas puras: Fa (p.75), Sol# (p.63) aunque si tuviéramos una escala mayor, prodríamos situar a las notas Fa# (p.162) y la nota La (p.150)
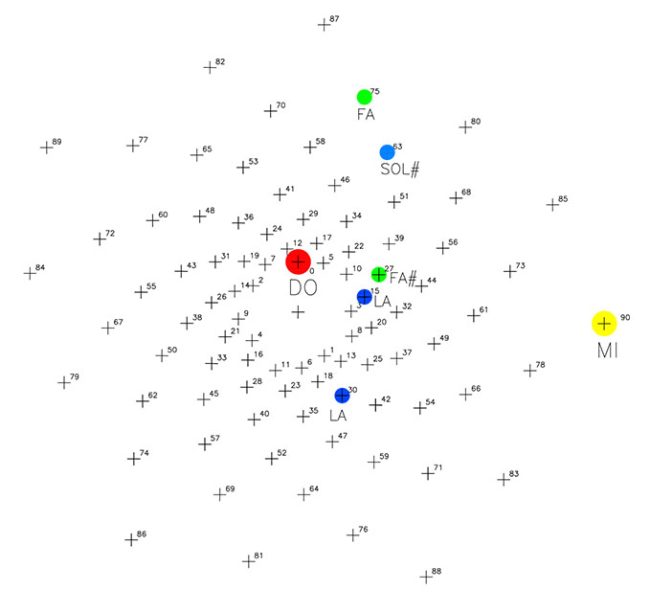
El estudio de las octavas interiores necesitaría otra escala de representación para poder examinar con más detalle ese juego de rayos o ejes que van definiendo las diversas notas musicales y que pasan por determinados puntos de ese universo √2 así como han «tocado» los puntos de los universos de φ y de ψ…
Cada nota siempre define un mismo eje en el círculo de 360º, pero cada una, en cada entorno de puntos característico de cada número geométrico, significa a un punto concreto y por ello, toma una diferente numeración relacionándose con sus próximos según diferentes «paraguas» como vimos en la F15 del artículo de las «Espirales del nº φ».
5.- IZQUIERDA Y DERECHA.
Como ya hemos visto en los dos casos anteriores, podemos trazar un eje vertical que une los puntos 0 y 360 o los ángulos 0º y 360º, y que diferencia entre el lado derecho del dibujo (D) y el lado izquierdo (I) y empezar a significar todos los puntos según su posición.
En la vuelta 1 se significan: 0) 0º – 1)149º (D) – 2) 298º (I)
En la segunda vuelta: 3) 87º (D) – 4) 236º (I)
En la tercera vuelta: 5) 25º(D) – 6) 174º (D) – 7) 323º (I)
En la cuarta vuelta: 8) 112º (D) – 9) 261º (I)
En la quinta vuelta: 10)50º (D) – 11)199º (I) – 12) 348º(I)
En la sexta vuelta: 13) 137º (D) -14) 286º (I)
En la séptima vuelta: 15) 75º (D) – 16) 224º (I)
En la octava vuelta: 17) 13º (D) -18)162º (D) – 19) 311º (I)
En la novena vuelta: 20) 100º (D) – 21) 249º (I)
En la décima vuelta: 22) 38º (D) – 23) 187º (I) – 24) 336º (I)
Y así sucesivamente hasta completar los 360 puntos .(2)
Hemos revisado los primeros 180 puntos y comprobado que las únicas posibilidades de combinación son:
DI=A
DDI=B
DII=C
y por ello, el sistema de crecimiento se ordena como:

Como ya hemos visto, la octava diatónica está formada por tres intervalos:
Tono mayor=9/8= A
Tono menor=10/9= B
Semitono diatónico=16/15= C
Establecemos las notas y los intervalos entre ellas; así entre Do-Re, Fa-Sol y La-Si funciona el tono
mayor A; entre Re-Mi y Sol-La es el tono menor B y entre MI-Fa y Si-Do funciona el semitono
diatónico C.
DO RE MI FA SOL LA SI DO RE MI FA SOL LA SI DO RE
A B C A B A C A B C A B A C A
Ordenando las vueltas:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A A B A C A A B A C A A B A B A C A A B A C A A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 …
A B A C A A B A C A A B A B A C A A B A C A A B …
Hemos revisado hasta la vuelta 61 y se reproduce este ritmo repetitivo: A ABACA ABACA …
Si nos fijamos en el orden definido por la gama diatónica, comprobamos que este ritmo comienza en el intervalo entre las notas Fa y Sol. Tal vez podríamos hablar de una posible gama ¿pentatónica? con el comienzo en modo FA. ¿Es una coincidencia que √2 tenga sus aproximaciones por defecto en la relación 7/5 y por exceso en la relación 10/7, en su cualidad musical como Fa#, y que el modo musical implícito en el desarrollo espacial de este número sea el modo Fa?
Esta coincidencia entre la disposición de los puntos definidos por √2 y el orden de los tonos de una posible gama pentatónica parece indicar la existencia de un orden subyacente entre tanta aparente diversidad…
Parece que mediante una observación más detenida sobre el nº √2 y su relación con la octava, se ponen de manifiesto casualidades y coincidencias, simetrías, ritmos y patrones que sugieren la existencia de órdenes y leyes no visibles en apariencia…
«Un punto, un patrón de vibración y la creación comienza…»
En el siguiente artículo, revisaremos al nº √3…
NOTAS:
1.- Recordar la definición de la octava angular:
DO = 0º
RE = 45º [(360ºx(9/8)=405º; 405º-360º=45º]
MI = 90º
FA = 120º
SOL = 180º
LA = 240º
SI = 315º [360ºx(15/8)=675º; 675º-360º=315º]
y por último la OCTAVA =360º.
2.- En los artículos dedicados al nº φ y al nº ψ, se ha desarrollado como nota a pie de artículo, el ciclo completo de puntos y los grados angulares correspondientes. En este caso, se evita la tediosa nota pues es fácilmente comprobable por el lector interesado.

Dejar un comentario