1.- INTRODUCCION.
En Parte 1 de «Espirales de números geométricos» no se presentó el dibujo completo del ciclo de 720 puntos con una razón de crecimiento mínima de 81/80 porque la falta de nitidez de la imagen y lo «pausado» de su movimiento angular de 0.5º, daba un resultado borroso para el formato de presentación elegido. Por ello, se va a utilizar el mismo formato anterior de √2 de los noventa primeros puntos y con la misma razón de crecimiento lineal 49/48 que se ha aplicado también para el estudio de los números φ y √2. Esta decisión permite que las escalas de los tres números sean «similares» aunque volvemos a insistir que los 90 primeros puntos para √3 sólo permite tener un atisbo de sus posibilidades. F1
Como en los casos anteriores de los números φ y √2, se produce una distribución de puntos en el espacio o en el plano, que su sola contemplación da indicios de las similitudes y diferencias con los anteriores números estudiados y aunque el formato elegido de unos 90 puntos no expresa la totalidad de este nº √3, sí permite un avance y una aproximación para su comprensión en su desarrollo angular.
Recordemos que estos 720 puntos de √3 equivalen a:
– Dieciocho veces el ciclo de ψ. (18×40 puntos= 720 puntos)
– Cinco veces el ciclo de φ. (5x144puntos=720 puntos)
– Dos veces el ciclo de √2. (2×360 puntos=720 puntos)
Así, queda establecido que el ciclo angular de √3 equivale a dieciocho veces el ciclo del nº plástico, cinco veces el ciclo del nº φ y duplica el ciclo de √2. Y nos indica no sólo a longitud del ciclo de √3 sino también la diferencia de velocidad entre estos números geométricos.
2.-ESPIRALES DE √3.
Siguiendo el mismo criterio de presentación ya establecido, exponemos en primer lugar las distintas espirales en función de su razón de crecimiento. Y como en las espirales de √2, no ha habido decisión a priori sino que el propio examen y sencillez en la organización de los puntos de √3 y su posible comparación con los otros números geométricos, es lo que ha decidido la selección de razones de crecimiento.
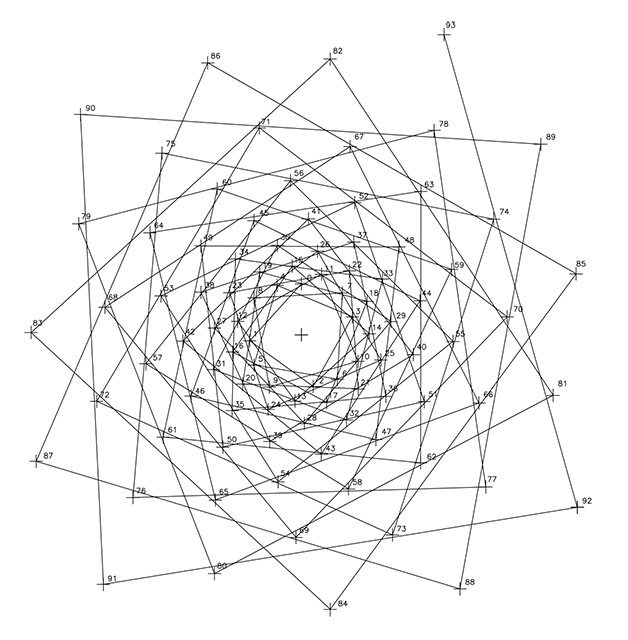
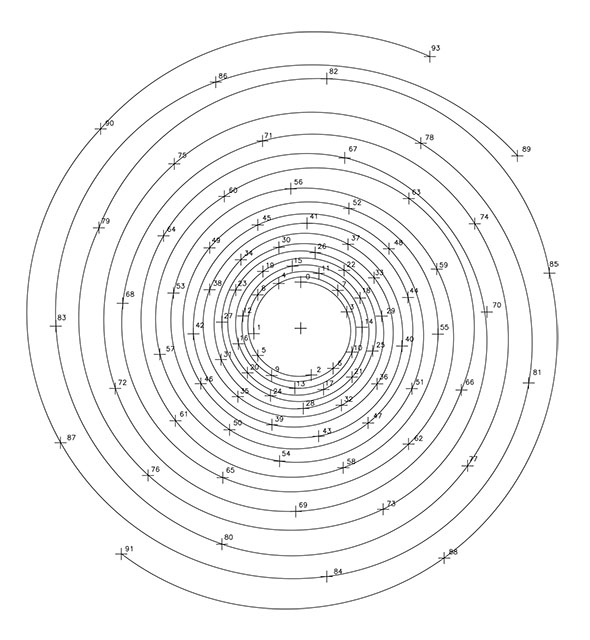
En la F2, se presenta la espiral de razón 1/1 unidos los puntos por líneas rectas, de carácter levógiro. Y en la F3, la espiral 1/3 que reproduce 3 espirales de sentido dextrógiro en este caso, mediante curvas.
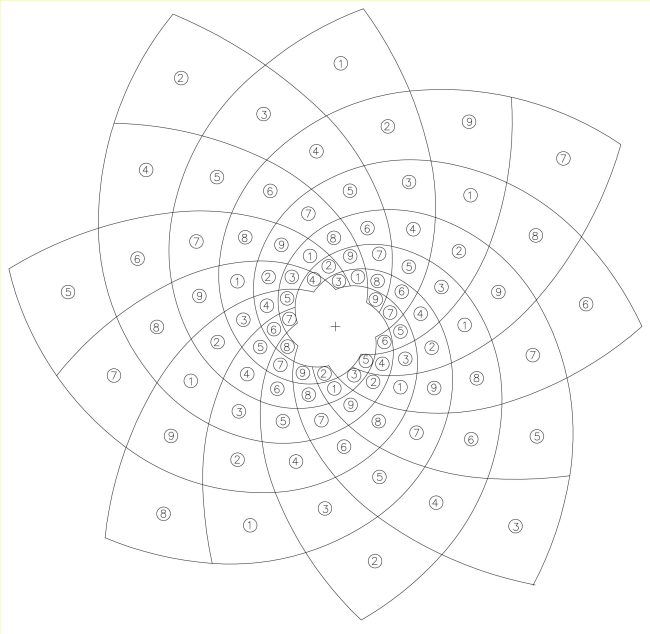
En las F4, F5, F6, F7 y F8 se presentan las cinco espirales de razón 1/5, todas ellas de sentido levógiro. Las exponemos como cinco imágenes porque recuerdan los dibujos de las siete espirales de razón 1/7 del nº φ al presentar ese «formato triangular»; y al igual que en las espirales φ en que la unión de los sucesivos vértices resultaba en nuevas espirales de razón 1/21, en este caso, reproducen en cada caso, tres espirales de razón 1/15.
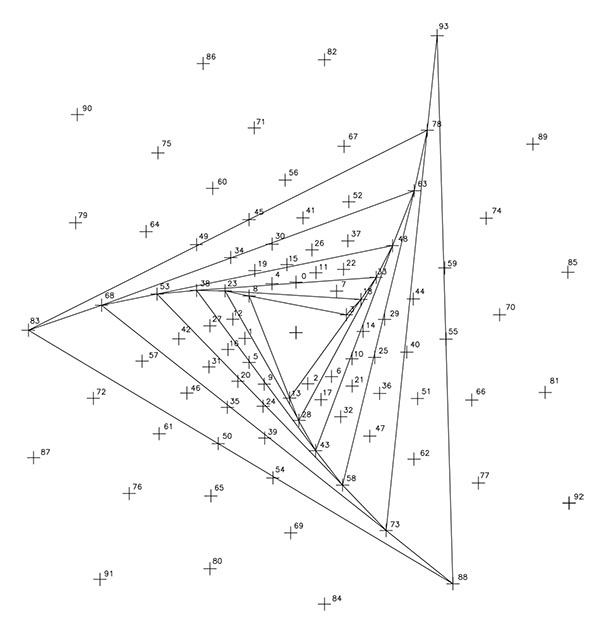
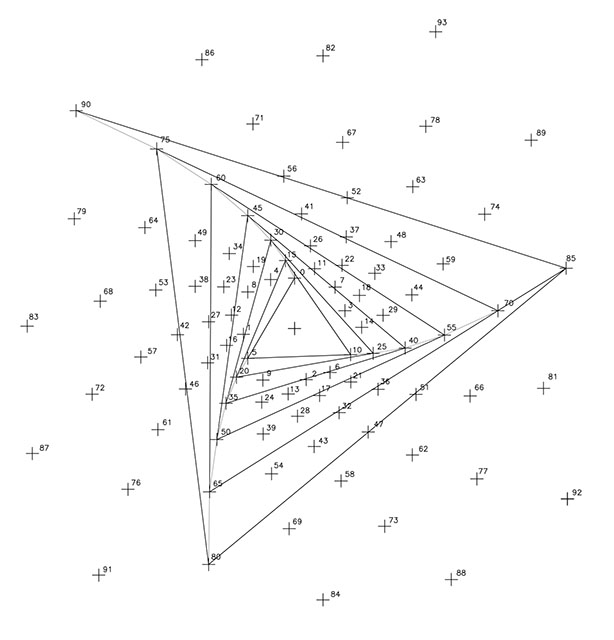
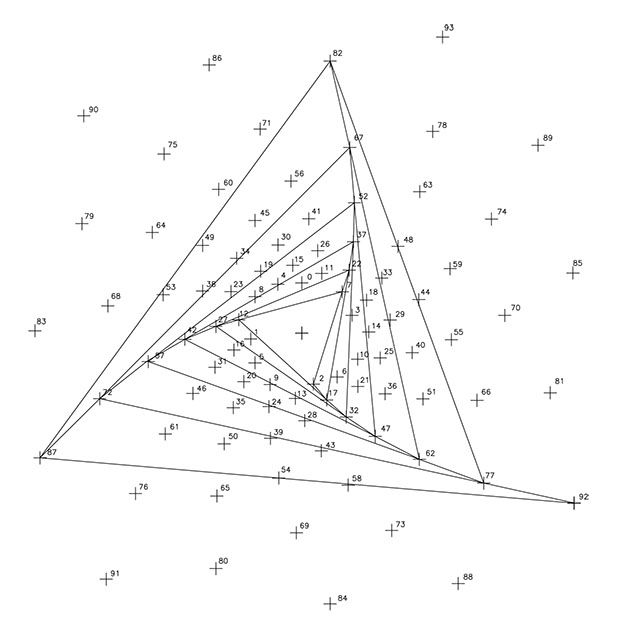
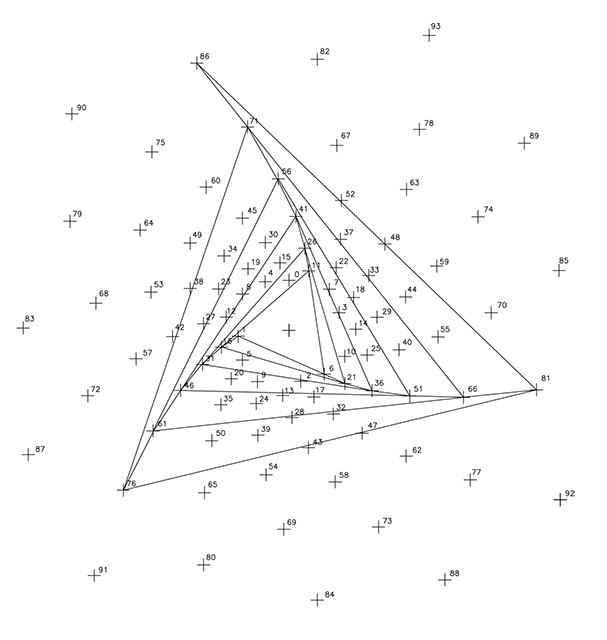
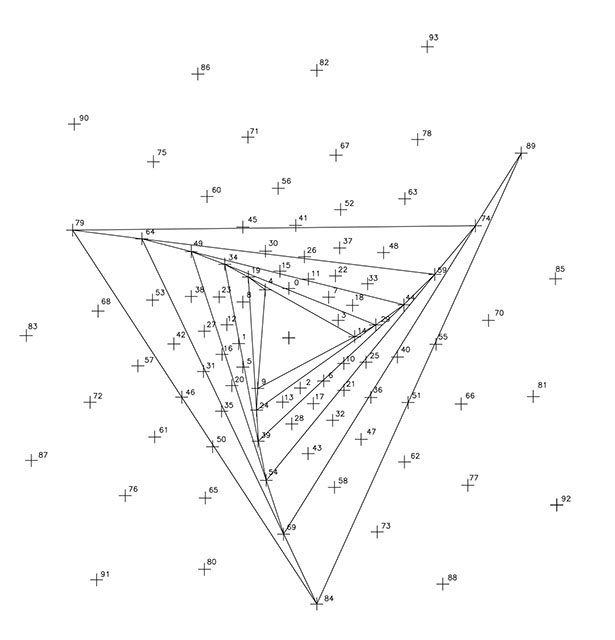
En las F9 y F10, se representan las once espirales de razón 1/11 y sentido dextrógiro y las 15 espirales de razón 1/15 y sentido levógiro; en este caso, ambos dibujos unen sus puntos por líneas rectas.
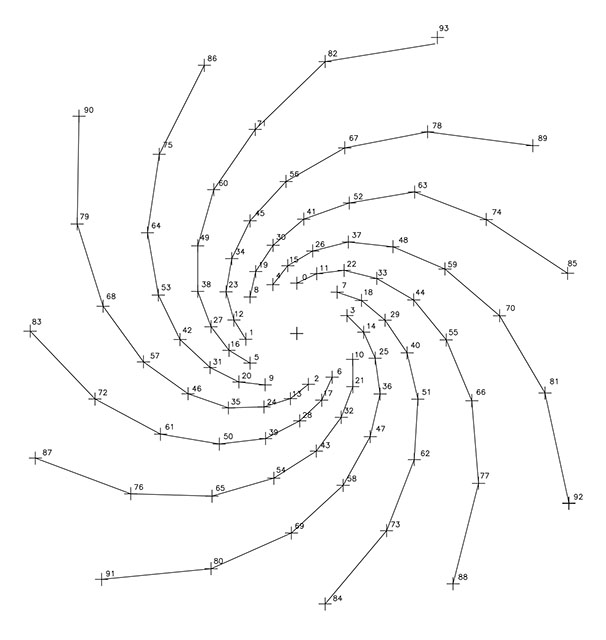
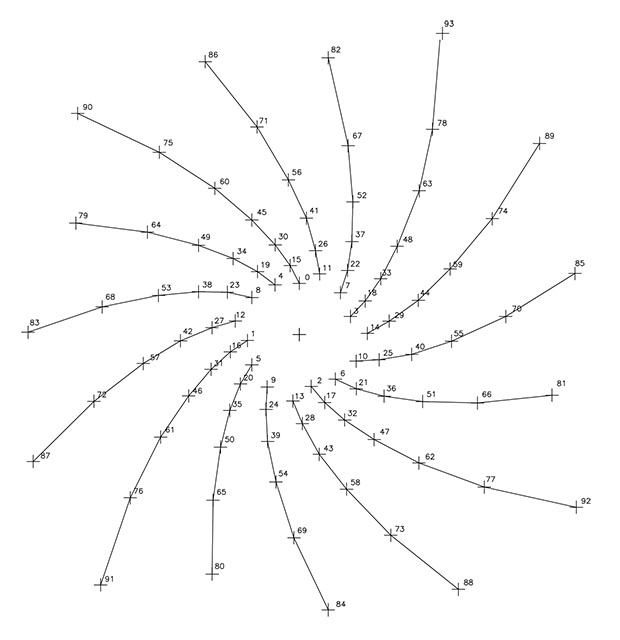
Y como en los anteriores casos ya estudiados, resultan simetrías implícitas entre las espirales dibujadas, en este caso, la superposición de las espirales de razón 1/11 y 1/15 . F11

3.- VALOR DE LOS SECTORES.
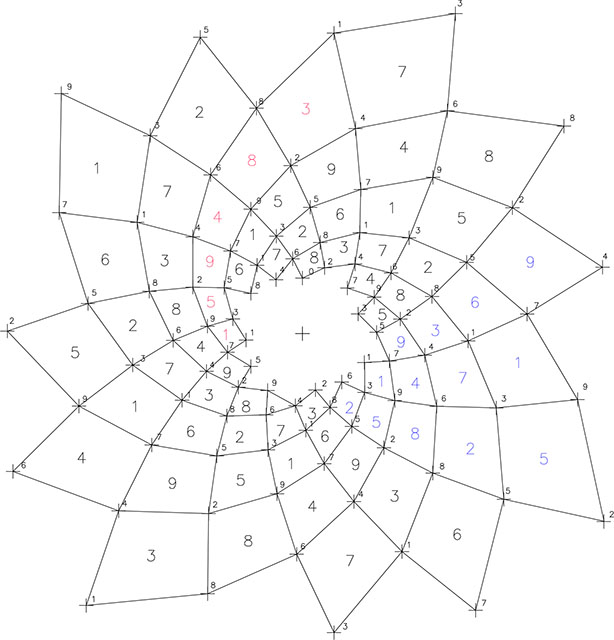
Otro de los aspectos tratados en los anteriores artículos, se corresponde con la reducción de la numeración de los puntos a los nueve primeros números. Aspecto que facilita la comprensión y diferenciación de las características formales y los “valores” implícitos en los sectores cuadran-gulares que resultan de la superposición de, en este caso, las espirales de razones 1/11 y 1/15.
Este proceso está planteado en la F12 con el mismo criterio que se ha utilizado en los casos anteriores de los nº φ y √2.
De nuevo podemos comprobar cómo las bandas dextrógiras formadas por las espirales 1/11, delimitadas por las 1/15 para la creación de los sectores cuadrangulares, están definidas por la serie1/5/9/4/8/… (suma de cuatro unidades a cada primer número de comienzo)… mientras que las bandas levógiras van marcadas por las tres series 1/4/7, 2/5/8 y 3/6/9 que ya podemos reconocer.
Hemos comparado, como imágenes, estos valores en los ámbitos de los nº φ, √2 y √3 en las F13, F14 y F15. La forma resultante de ellas es, por supuesto diferente pero a la vez, tienen muchas similitudes porque el proceso es el mismo: la distribución de los “valores” en los sectores cuadrangulares son iguales en los casos de √2 y de √3, F13 y F14, siguiendo las bandas levógiras de expansión triádica de 1/4/7, 2/5/8 y 3/6/9; pero si nos fijamos en el “valor” numérico de los sectores dextrógiros, veremos que en el dibujo de √2, las bandas van reproduciendo la alternancia de números pares e impares mientras que en el dibujo de la derecha para √3, las bandas dextrógiras reproducen el movimiento numérico de múltiplos de 4 y reducción a los nueve primeros números.


F14. Valor de los sectores cuadrangulares de √3 en la espirales 1/11 y 1/15.
En el caso del nº φ, los valores cuadrangulares que resultan provienen de la superposición de las espirales 1/8 y 1/13. Las bandas dextrógiras siguen una secuencia basada en la alternancia de los números impares y pares 1/3/5/7/9/2/4/6/8… y las bandas levógiras siguen la secuencia numérica 1/2/3/4/5/6/7/…
Recordemos que aunque los dibujos tiene una escala similar, la escala real es diferente y así la imagen de φ debería representarse como cinco veces menor que la de √3 y a la imagen de √2 le correspondería ser la mitad de la de √3.
El apartado 4 de los anteriores artículos dedicados a los números ψ, φ y √2 titulado «Espirales y Octava», desarrollado en los dos primeros números y apuntado en el caso de √2, no va a ser desarrollado por tema de formato y escala. Sí podemos decir que el punto 90 de cierre de este estudio corresponde a la nota Si de la gama diatónica y recordemos que este punto 90 en la distribución de √2, corresponde a la nota Mi de la gama diatónica.
Ya hemos visto que la distribución de los “ejes” de la diferentes notas de la octava al recorrer cada escenario numérico, ha calificado puntos concretos como “asiento” de sonidos y/o frecuencias de las notas de la gama musical. Este número √3, al tener un corrimiento angular de 0.5º, y por lo que hemos podido comprobar en un repaso a los primeros 180 puntos, podemos apuntar que la totalidad de las gamas diatónica y cromática están representadas en este largo ciclo de 720 puntos.
4.- IZQUIERDA Y DERECHA.
Como hemos visto hasta ahora en los anteriores artículos, trazamos un eje vertical central que une los puntos definidos por 0º y 360º y que va a diferenciar entre los lados derecho e izquierdo del dibujo.
Así, en la vuelta 1 se significan los puntos: 0) 0º 1) 263,5º (I)
En la vuelta 2: 2)167º (D)
En la vuelta 3: 3) 70,5º (D) 4) 334º (I)
En la vuelta 4: 5) 237,5º (I)
En la vuelta 5: 6) 141º (D)
En la vuelta 6: 7) 44,5º (D) 8) 308º (I)
En la vuelta 7: 9) 211,5º (I)
En la vuelta 8: 10) 115º (D)
En la vuelta 9: 11) 18,5º (D) 12) 282º (I)
En la vuelta 10: 13) 185,5º (I)
En la vuelta 11: 14) 89º (D) 15) 352,5º (I)
En la vuelta 12: 16) 256º (I)
En la vuelta 13: 17) 159,5º (D)
En la vuelta 14: 18) 63º (D) 19) 326,5º (I)
En las vuelta 15: 20)230º (I)
En la vuelta 16: 21)133,5º (D)
Y así sucesivamente… Hemos revisado los primeros 90 puntos y comprobado que las únicas posibilidades son:
I=A
D=B
DI=C
El sistema de crecimiento se ordena:
V1 V2 V3 V4 V5 V6 V7 V8 V9
1(I) 2(D) 3(D)-4(I) 5(I) 6(D) 7(D)-8(I) 9(I) 10(D) 11(D)-12(I)
A B C A B C A B C
V10 V11 V12 V13 V14 V15 V16
13(I) 14(D)-15(I) 16(I) 17(D) 18(D)-19(I) 20(I) 21(D)
A C A B C A B
V17 V18 V19 V20
22(D)-23(I) 24((I) 25(D) 26(D)-27(I)
C A B C
V21 V22 V23 V24…
28(D) 29(D)-30(I) 31((I) 32(D)…
B C A B
Como ya hemos visto anteriormente, la octava diatónica está formada por tres intervalos:
Tono mayor: A
Tono menor = B
Semitono diátonico= C
Establecemos las notas y los intervalos entre ellas:
DO RE MI FA SOL LA SI DO RE MI FA SOL LA SI DO RE
A B C A B A C A B C A B A C A
En este caso, el sistema de crecimiento produce una primera triada que se repite tres veces y a continuación se reproduce el ritmo de la escala diatónica partiendo del modo LA:
A B C A B C A B C A C A B C A B
C A B C B C A B C A B C
A B C B C A B C A B C A C A B C A B
C A B C A C A B C A B
C A B C B C A B …
este es el ritmo que marca √3 hasta la vuelta 66 y el punto 90… Puede atisbarse ya un orden en este inicio pero recordemos que esto que estamos analizando corresponde a una octava parte del ciclo completo…
Estas coincidencias entre la disposición de los puntos definidos por la razón angular de √3 y el orden de los tonos en la octava diatónica, confirma de nuevo, la existencia de un orden subyacente entre tanta aparente diversidad..
6.-UNAS PRIMERAS CONCLUSIONES.
El punto quinto anterior común a los cuatro números geométricos, permite vislumbrar unos ciertos órdenes o ritmos característicos en la posición y distribución de los puntos de cada escenario.
Curiosas «coincidencias» de ritmos entre estos números geométricos y la gama musical u octava…
– El ritmo del nº φ, simétrico a la mitad del ciclo, que comienza:
A C A B C A B A B C A B C …
establece en modo La las siete etapas de la gama diatónica, seguido dos veces de los tres primeros intervalos, con un podríamos llamar, Do/Re/Mi.
– El ritmo de √2 que comienza:
A A B A C A A B A C A A B A B A C A A B A C A A B …
permite plantear un comienzo o atisbo de su ritmo basado en modo Fa las cinco etapas de la gama ¿pentatónica?, pero su estudio completo queda fuera de los límites de esta investigación.
– El ritmo de √3 que, como acabamos de ver, comienza:
A B C A B C A B C A C A B C A B …
establece un comienzo con la triada de los tres primeros intervalos, otro Do/Re/Mi, y las siete etapas o notas de la gama diatónica comenzando en modo La. De nuevo al igual que con √2, su estudio queda fuera de los límites de esta investigación. El hecho de tener el crecimiento más lento y el ciclo de mayor longitud, sólo permite intuir la existencia de un ritmo más complejo. También está latente como en √2, la posibilidad de nuevas simetrías a la llegada de ambos la mitad del ciclo o a los 180º de su movimiento angular.
– El ritmo del nº ψ, que mantiene siempre sus diferencias con respecto a los tres anteriores, comienza y finaliza:
C C C C C C A B B B B B B B
reproduciendo una «reverberación» triádica repetitiva (D I I o D I I) desde el centro hacia los dos extremos de origen y final del ciclo con una simetría central en la mitad del ciclo. Simetría difícil de apreciar dada la forma de «trisquel» que sus puntos toman en su distribución del ciclo.
Esto es, partiendo de la posición de cada punto en cada ciclo respecto a un eje central, vemos que la ordenación de ellos toma desarrollos y ritmos característicos en cada número geométrico…
Y surge una cuestión: ¿Qué pasaría si cambiásemos el eje de giro y lo realineásemos con otra dirección espacial? Mantendrían estos números esos ritmos tan característicos?
Sí podemos apuntar que los puntos definidos en el plano o en el espacio intrínsecamente serían los mismos pero su «posición» con respecto al nuevo eje de referencia supondría otra nueva distribución pues establecería un nuevo escenario de derecha y izquierda… Tomemos, por ejemplo, una rotación angular de 315º respecto al anterior eje. Nuevo eje que define la nota Si de la octava angular en los cuatro escenarios. Las F16, F17, F18 y F19 dibujan el nuevo eje de alineación y la diferente posición izquierda – derecha que esto conlleva en el conjunto de los puntos de los cuatro escenarios.


F17. Representación parcial de los puntos √3 y nuevo eje donde el punto 90 es la Si.
De nuevo recordar que las escalas son similares para que se pueda comprobar en los diferen-tes dibujos que se presentan, que esta nueva alineación pasa por determinados puntos de cada escenario.
Vamos a examinar el escenario del nº φ y para la exposición, se han estudiado los primeros 60 puntos en sus nuevas «posiciones» centrándonos en las primeras 16 vueltas del ciclo. F19
Así, el nuevo eje ha rotado 315º con respecto al estudio anterior y
en la vuelta1: P0) D P1) I P2) I
En la vuelta 2: P3) D P4) I
En la vuelta 3: P5) D P6) D P7) I
En la vuelta 4: P8) D P9) I P10) I
En la vuelta 5: P11) D P12) I
En la vuelta 6: P13) D P14) D. P15) I
En la vuelta 7: P16) D P17) I P18) 0º –
En la vuelta 8: P19) D P20) I
En la vuelta 9: P21) D P22) I P23) I
En la vuelta 10: P24) D P25) I
En la vuelta 11: P26) D P27) D P28) I
En la vuelta 12: P29) D P30) I P31) I
En la vuelta 13: P32) D P33) I
En la vuelta 14: P34) D P35) D P36) I
En la vuelta 15: P37) D P38) I
En la vuelta 16: P39) D P40) D P41) I
y así, sucesivamente hasta la vuelta 55… Las únicas posibilidades de combinación son:
– DI= A
– DDI= B
– DII= C
y por ello, el sistema de crecimiento se ordena:
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16…
C A B C A B A A C A B C A B A B…
Recordemos que la octava diatónica está formada por los tres intervalos: Tono mayor= A, tono menor= B y semitono diatónico= C y también recordemos estos intervalos en la gama diatónica.
DO RE MI FA SOL LA SI DO RE MI FA SOL LA SI DO
A B C A B A C A B C A B A C
Esto es, la nueva alineación en las primeras 16 vueltas, reproduce en las 7 primeras vueltas el orden de intervalos de la gama diatónica en modo Si, en la siguiente vuelta sólo hay un intervalo y a partir de la novena vuelta repite de nuevo el orden de intervalos en modo SI… Algo así como:
C A B C A B A A
C A B C A B A B
C A B C A …
Recordemos que la anterior alineación con el eje central reproducía en las primeras 7 vueltas el orden de intervalos de la gama diatónica en modo LA, en las seis siguientes repetía un doble A B C y a partir de la 14 vuelta volvía a repetir el orden de los 7 intervalos en modo LA…
Esto apunta a que si volvemos a observar las distintas espirales que hemos ido exponiendo, el sentido del giro viene decidido por ese eje central (visible o invisible es igual), que define un mundo de «derechas e izquierdas», «dextrógiro o levógiro», un mundo polarizado de «posiciones» donde esa misma idea posicional depende del eje de referencia elegido.
Patrones de comportamiento recurrentes y subyacentes en ese movimiento expansivo de la creación… Existencia de órdenes invisibles más allá de las apariencias…
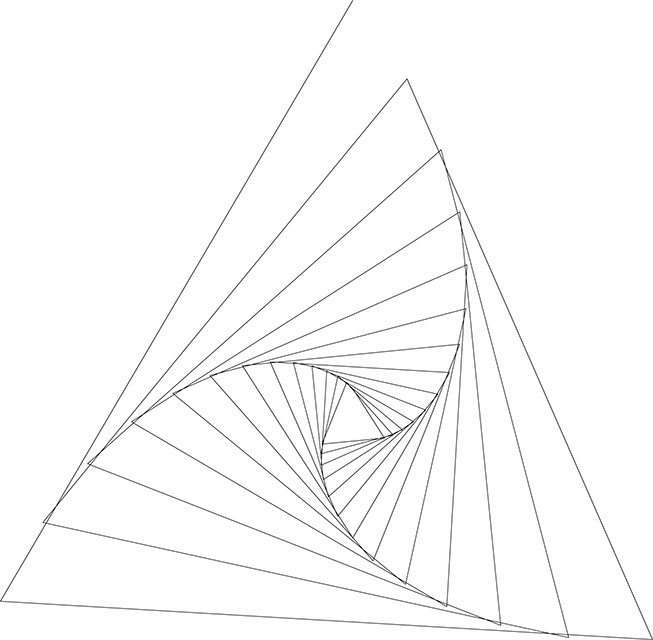
Pausamos este ciclo dedicado a las Espirales con esa imagen tan potente y sintética de espiral de razón 1/1 del nº ψ en la que una línea toma la forma de un aparente triángulo rotando sobre un centro invisible convirtiéndose en casi un símbolo…
Maria Luisa Lopez Sardá
Julio 2023



Dejar un comentario