1.- INTRODUCCIÓN.-
Como ya hemos comentado en un artículo anterior: “Espirales de los números geométricos. Parte 1”, comenzamos el estudio con la espirales correspondientes al nº Φ y ángulo 137,5º. Daremos un somero repaso en esta Introducción a lo que suponemos ya conocido y a continuación, en los siguientes apartados, centraremos nuevos aspectos que también desarrolla-remos para los siguientes números geométricos.
Recordemos que la proporción lineal de crecimiento ha sido 49/48 y la relación angular, en este caso, de 137,5º. Es decir, la proporción aurea cierra su crecimiento angular en 55 vueltas y 144 puntos han sido definidos en el recorrido.
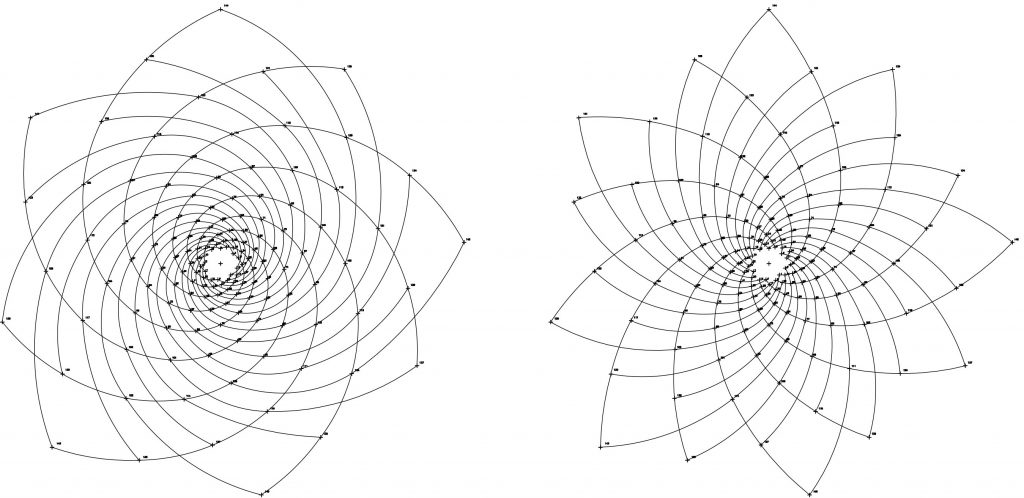
Así, retomamos la figura 3 del artículo anterior y recordamos que empezamos desde el eje vertical con una longitud 1cm que definió el punto 0, el punto 1 quedó definido por un giro de 137,5º y un crecimiento lineal de 1x(49/48) cm. El punto 2 tuvo un crecimiento lineal de1x(49/48)x(49/48)cm, etc. Fig.1.
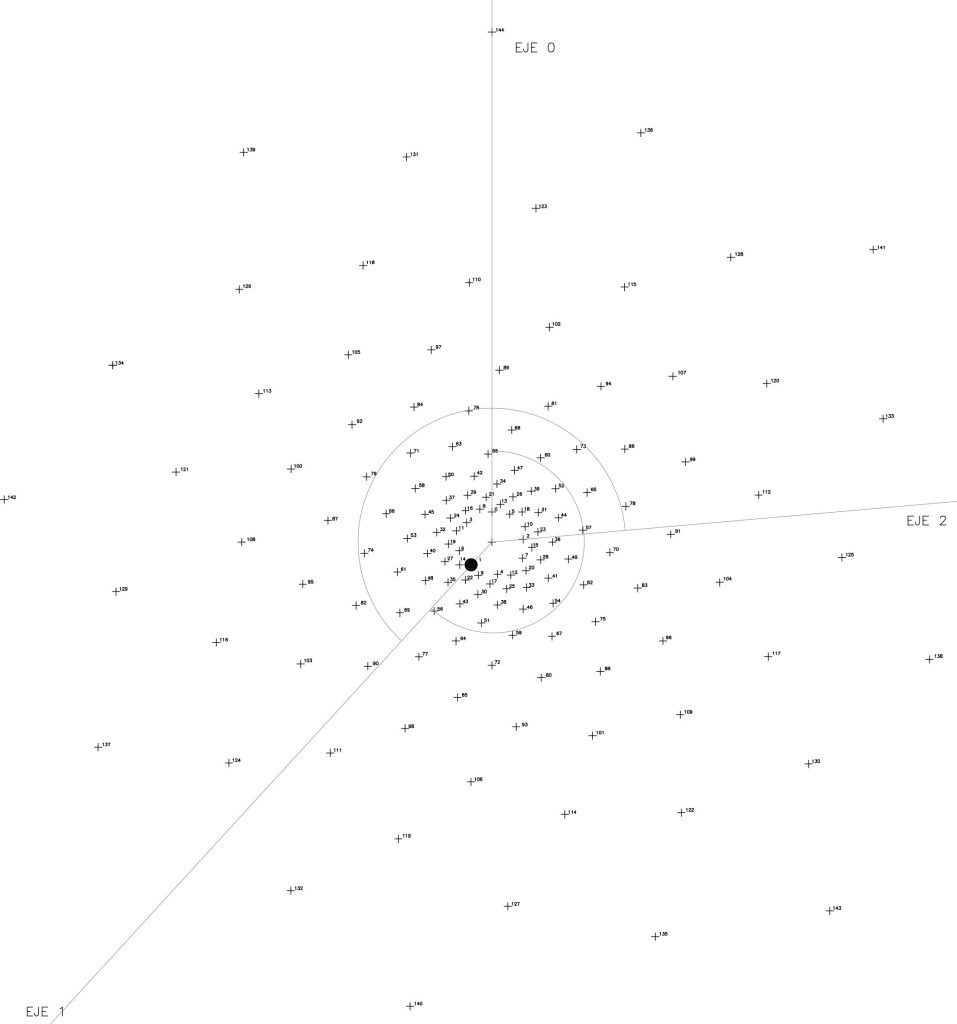
Pero no olvidemos el crecimiento angular de Φ mediante 222,5º. El fondo de puntos de ambos desarrollos son en apariencia muy similares aunque funcionando de manera especular. Así por ejemplo, el penúltimo punto 143 de la serie de Φ=137,5º, Fig.1, se corresponde angularmente con el punto 1 de la serie Φ=222,5º. Fig.2
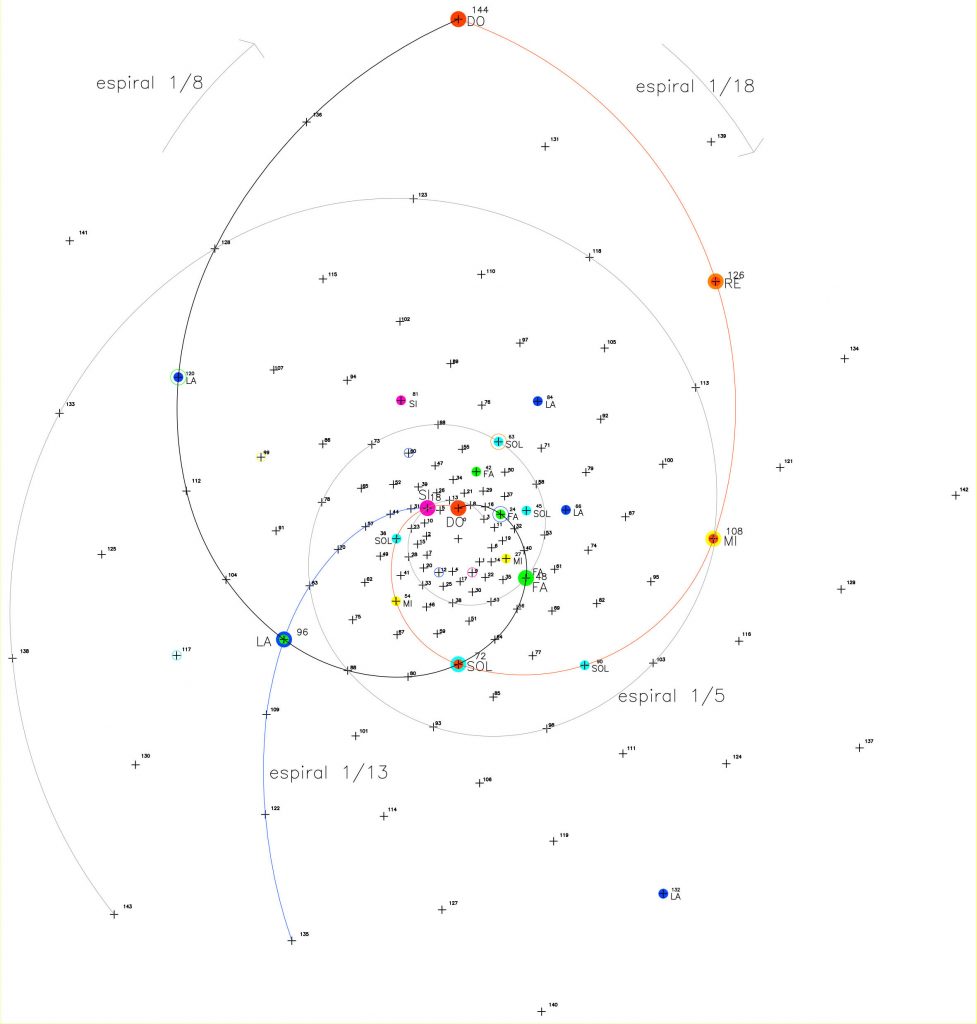
Centrándonos en la figura 1, la serie de Fibonacci: 1, 2, 3, 5, 8, 13, 21… va a definir el sistema de crecimiento para dibujar las diferentes espirales,1/3,1/5,1/8, 1/13, 1/21, 1/34, 1/55, etc. Es decir, la espiral 1/3 contiene 3 espirales que comienzan con los puntos 0, 1 y 2; la espiral 1/5 contiene 5 espirales que comienzan con los puntos 0, 4, 9, 14, 19 y así sucesivamente.
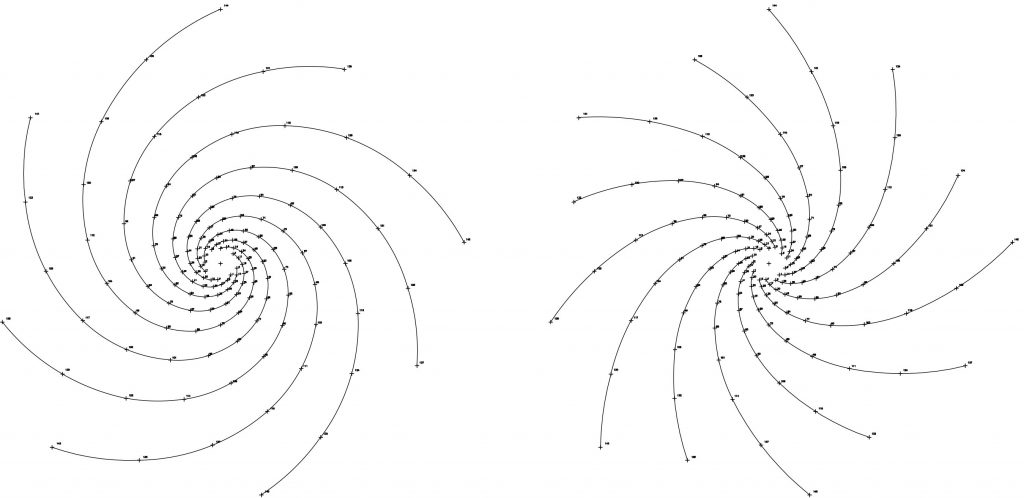
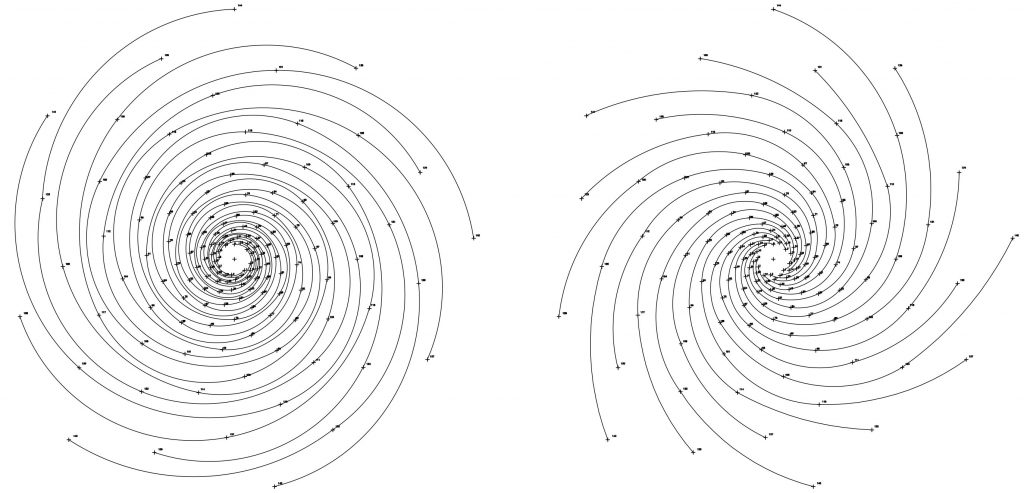
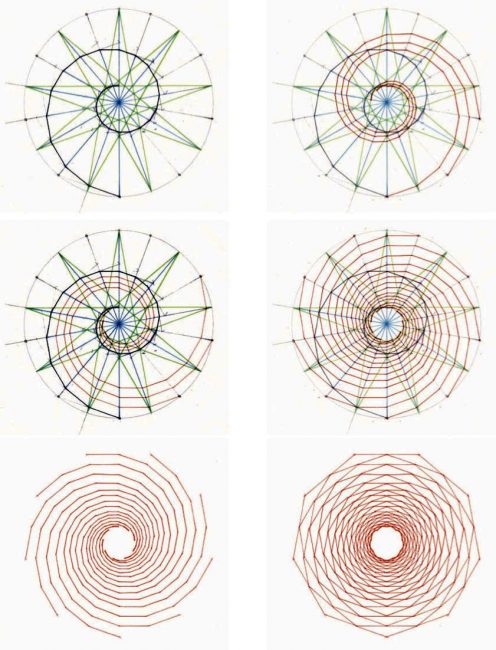
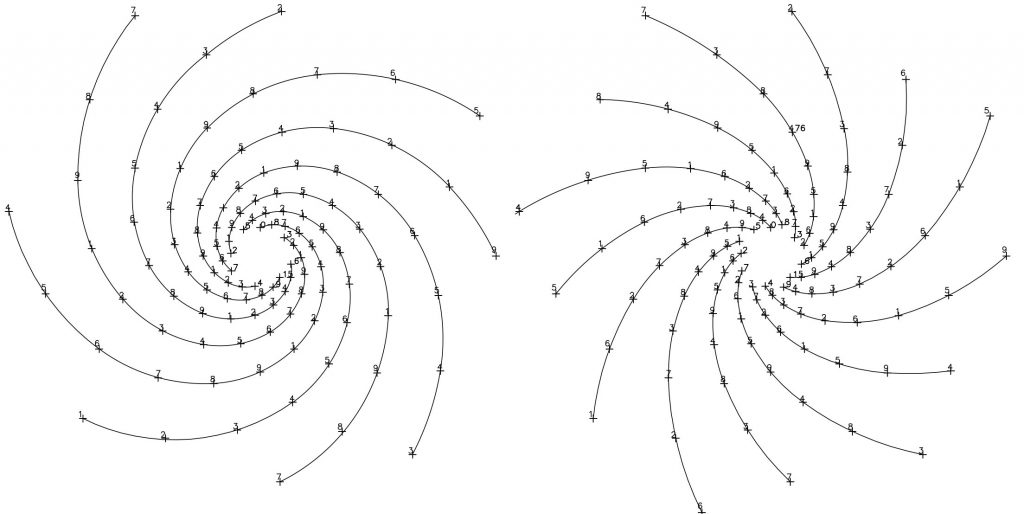
En estos seis primeros dibujos podemos comprobar las alternancias en el giro. Fig. 3, 4, 5.
Las espirales 1/3,1/8 y 1/21 son dextrógiras y las espirales 1/5, 1/13 y 1/34 son levógiras. Una alternancia de giro entre el orden de los números de la serie y, como ya hemos visto, el número que fija el ritmo define el nº de espirales existentes en cada dibujo… si seguimos la serie, la relación 1/13 contiene 13 espirales, la relación 1/21 contiene 21 espirales y así sucesivamente.
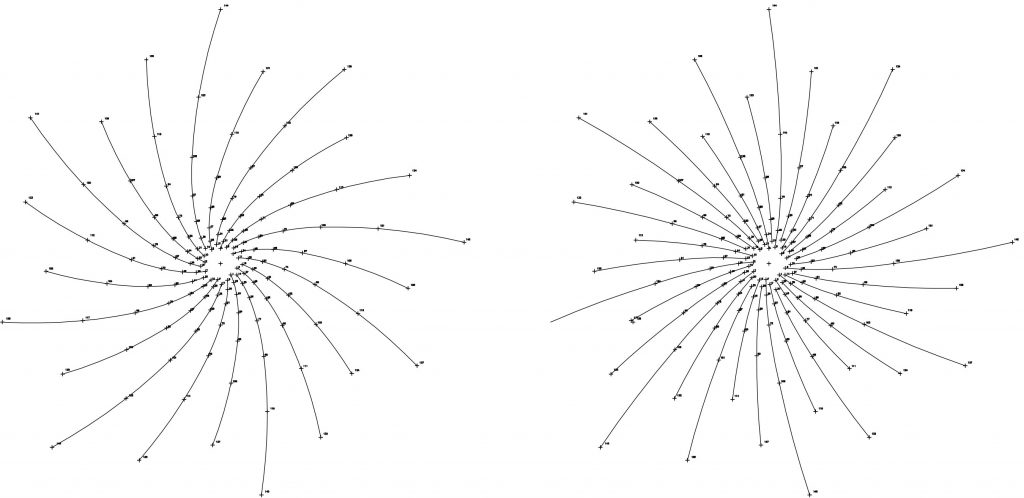
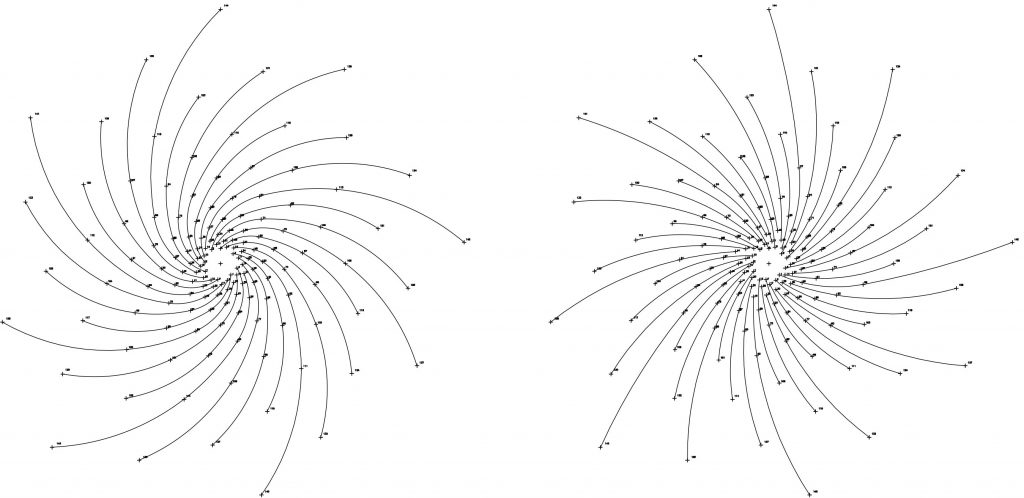
Sobre el mismo fondo de puntos, también podemos establecer las espirales de potencias de Φ siguiendo el mismo criterio: 1, 3, 4, 7, 11, 18, 29, 47,… En este caso, los dibujos corresponden a las espirales 1/11, 1/18, 1/29 y 1/47, las correspondientes a la serie 1/7 las veremos con más detalle en un siguiente apartado. Fig.6 y 7.
De nuevo, podemos comprobar las alternancias de giro; las espirales 1/11 y 1/29 son dextrógiras mientras que las espirales 1/18 y 1/47 son levógiras y que el nº que fija el ritmo define el número de espirales existentes, es decir, la relación de crecimiento 1/11 contiene once espirales y así sucesivamente.
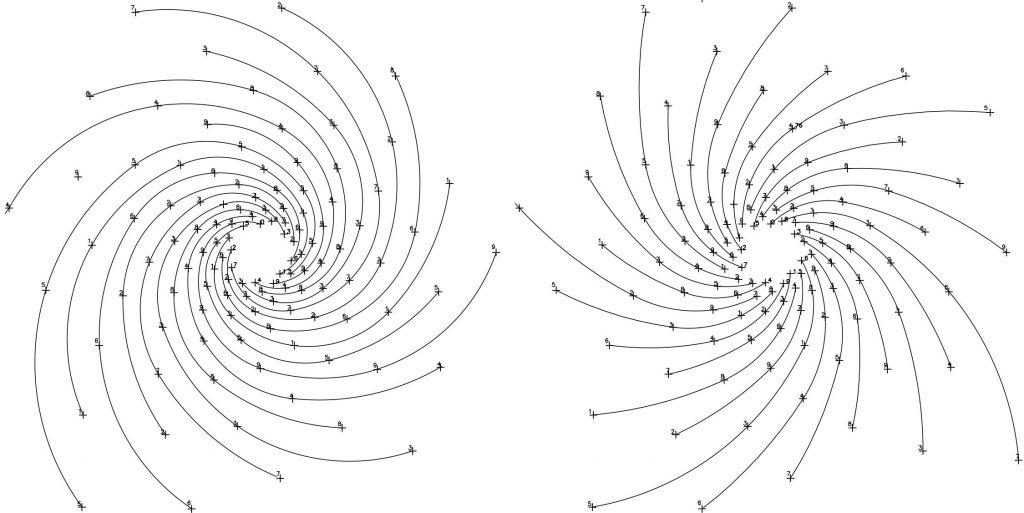
Así mismo, podemos comprobar las simetrías existentes entre ambas series (Fibonacci y Lucas). Por ejemplo, la espiral 1/8 es simétrica con respecto a la espiral 1/18, así como la espiral 1/13 se corresponde con la espiral 1/29 y la espiral 1/21 se corresponde con la espiral 1/47. Figs 8 y 9.
Esto trae al recuerdo el libro «The Hidden Geometry of Flowers» (1) de Keith Critchlow: un estudio y análisis de las flores como fenómeno total de floración: desde el brote de la semilla a su fruto final. Existencia de las flores planteadas como reflejos de verdades intemporales, como procesos pitágoricos de existencia desde la semilla (punto), al tallo de crecimiento (linea) donde surgen las hojas (plano) y finalmente la forma de la flor delinea un sólido (campo de tres dimensiones) para dar luego el fruto (campo tetradimensional).
Critchlow define estos dibujos como «patrones» geométricos, patrón como el gran recordatorio, como el despertar del recuerdo de las verdades permanentes. Más adelante volveremos sobre ello. Fig.10.
Todo el desarrollo que estamos exponiendo se supone ampliamente conocido. Su inclusión en este texto es un somero repaso o recuerdo para centrar el desarrollo de nuestro proceso.
Si reducimos la numeración de los 144 puntos hallados a los 9 primeros números (por ejemplo, 34=3+4=7, 108=1+8=9, 75=7+5=12=3, etc) sustituyéndolos y tomando una zona parcial del conjunto y volvemos a examinar el ritmo de las espirales, encontramos curiosas coincidencias.
Así por ejemplo, en la espiral 1/3, una sigue el ritmo 1/4/7/1/4/7…, otra el ritmo 2/5/8/2/5/8… y la tercera 3/6/9/3/6/9…Fig.11.
En la espiral 1/8 los puntos de sus ocho espirales siguen la secuencia numérica 1/2/3/4/5/6/7/8/9… y en la espiral 1/18, sus dieciocho espirales se definen por un mismo número repetido, por ejemplo 3/3/3/… o 7/7/7…Fig.12 Fig.13
En la espiral 1/29, las 29 espirales repiten el mismo ritmo que las de 1/13 pero si una empieza por los números impares 1/3/5/7… la otra comienza con los pares 2/4/6/8… (2)
2.- ESPIRALES Y OCTAVA.
En el artículo anterior, introdujimos un nuevo dato o filtro de ordenación al considerar el crecimiento angular de la octava.
Esto es, si la distribución angular de la octava la superponemos a ese fondo de puntos definidos por el crecimiento angular de Φ, nos encontramos que, en orden ascendente, si tomamos la nota Do o Unísono como 0º y punto 0 de comienzo:
– la vuelta 1 define el Punto 0 = DO o UNISONO= 0º
– en la vuelta 7 se define el Punto 18 = SI =315º
– en la vuelta 19, el Punto 48 = FA =120º
– en la vuelta 28, el Punto 72 = SOL = 180º
– en la vuelta 37, el Punto 96 = LA =240º
– en la vuelta 42, el Punto 108 = MI = 90º
– en la vuelta 49, el Punto 126 = RE = 45º
– y por último en la vuelta 55, queda definido el Punto 144 = DO u OCTAVA = 360º. Fig.14 (3)
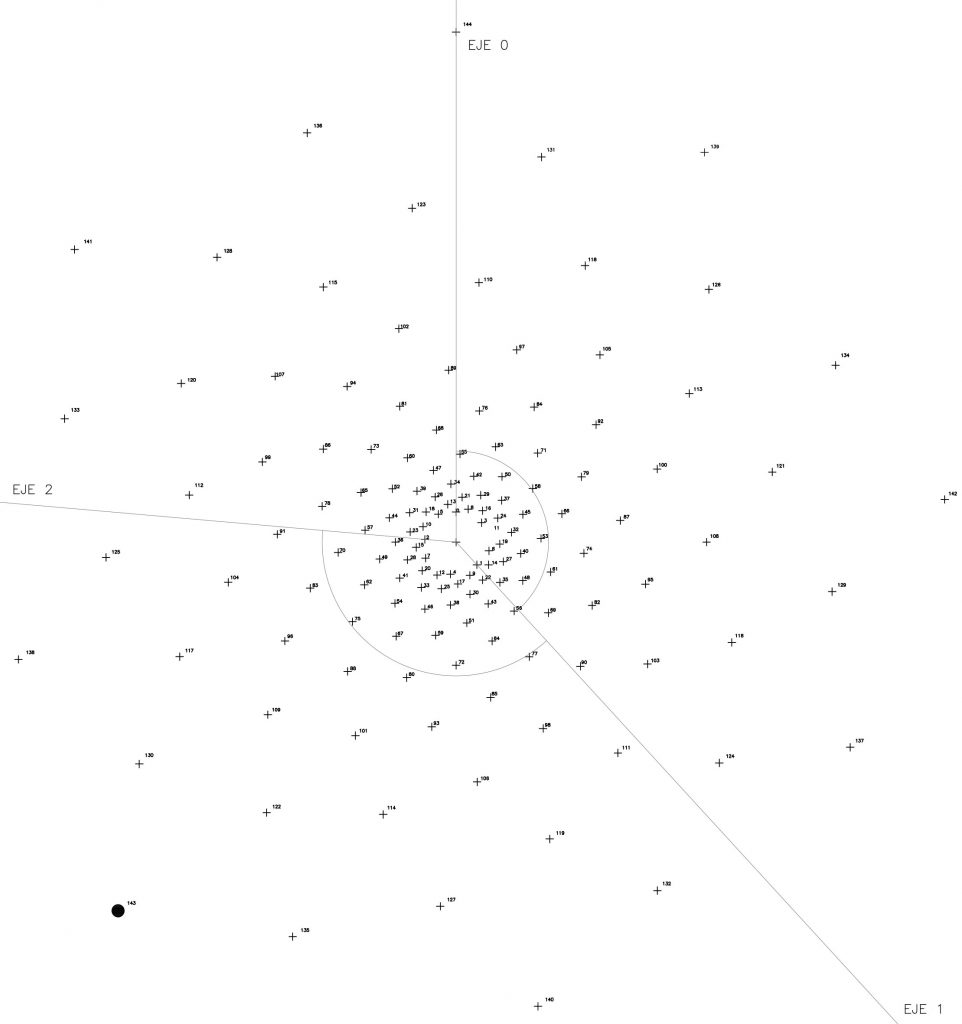
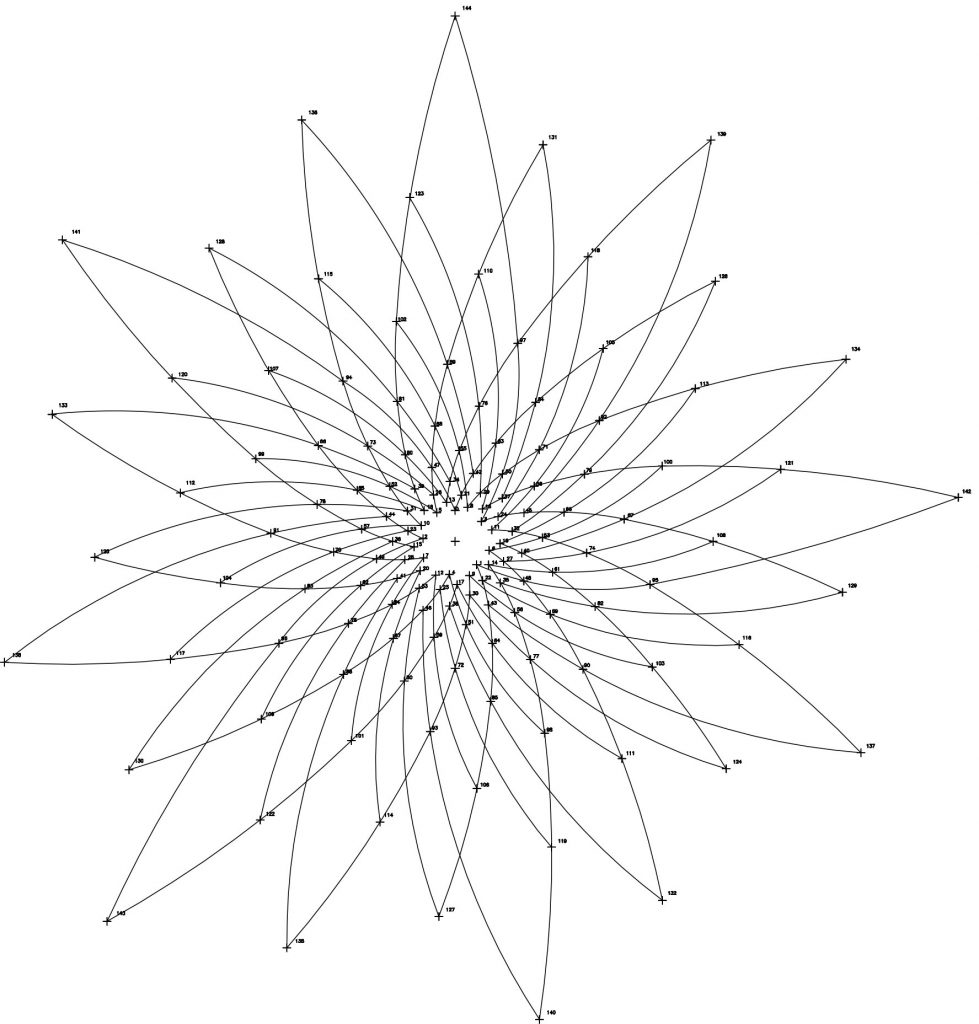
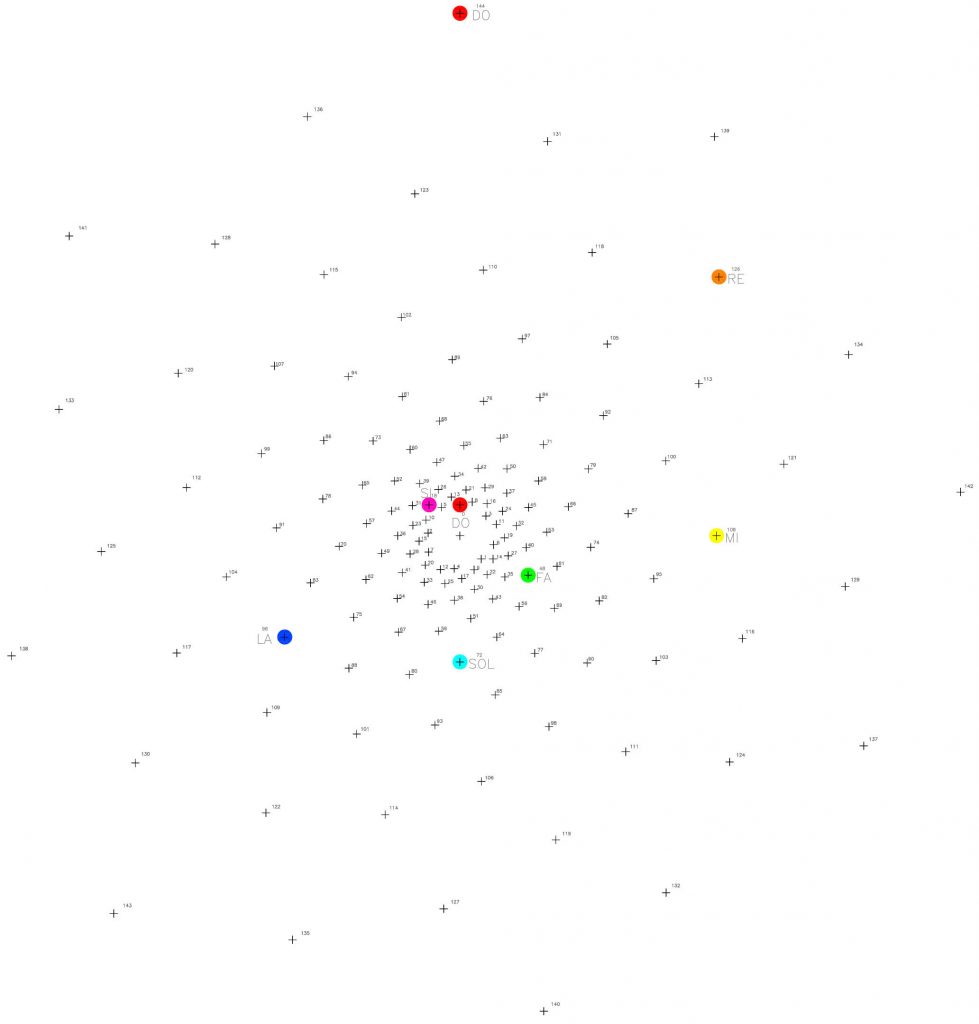
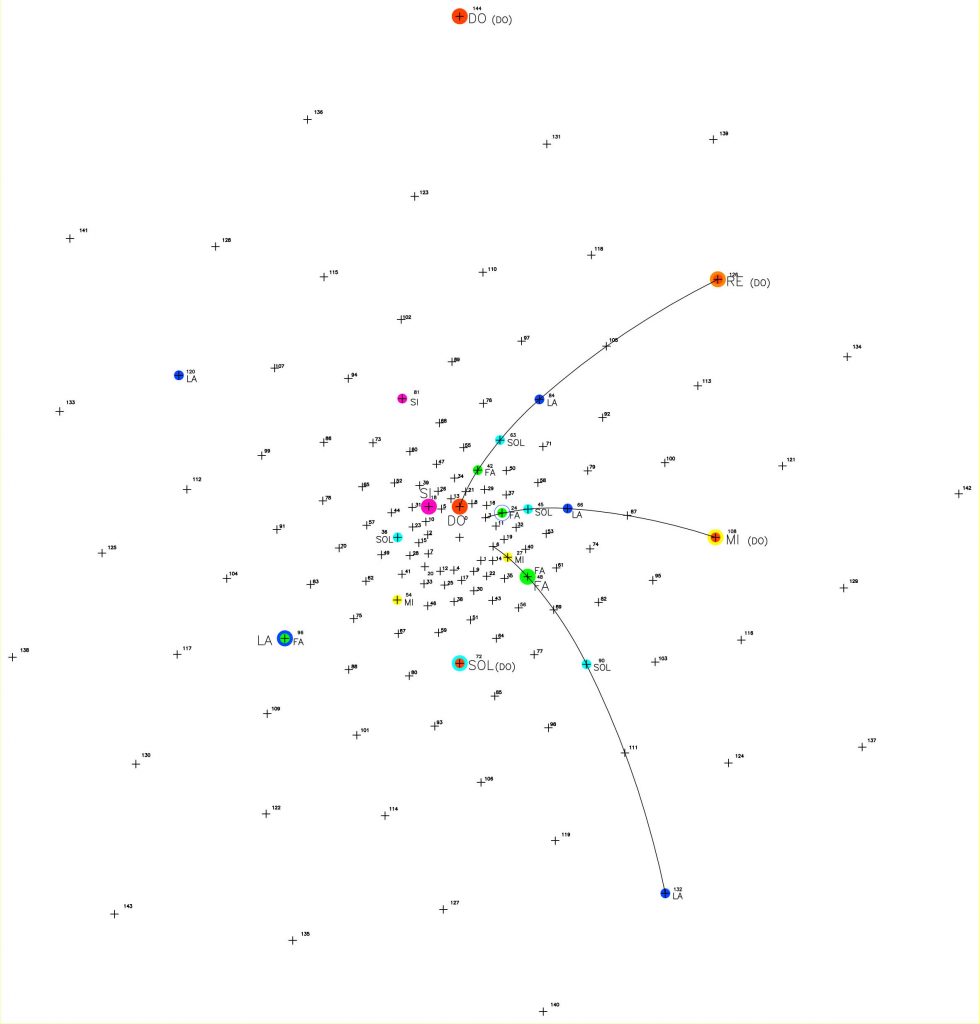
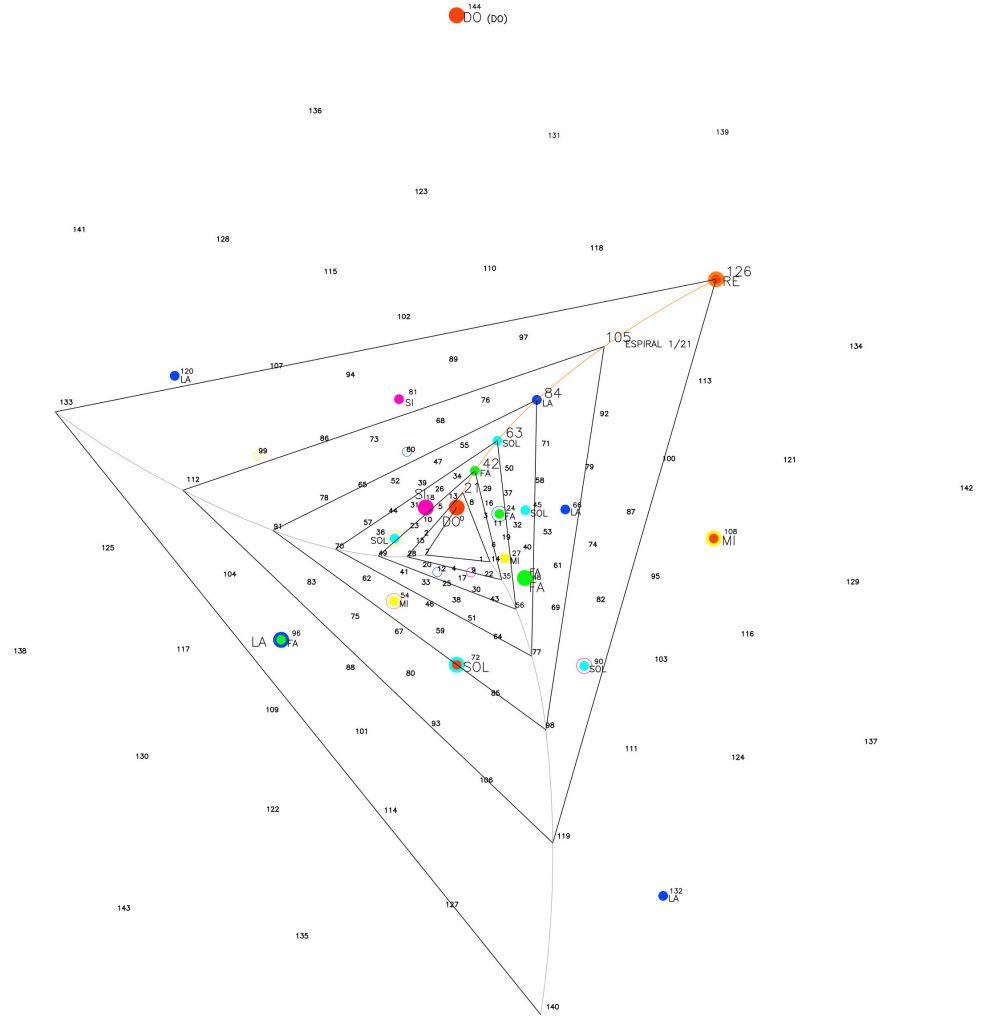
Podemos examinar en la figura 15 que una serie de puntos comienzan a sobresalir sobre ese fondo de puntos o estrellas, y si los observamos, intuitivamente parece existir un cierto orden dentro de ese fondo necesariamente ordenado por la expansión de Φ. Cada punto significado tiene una relación de “vecindad o proximidad” con los que le rodean.
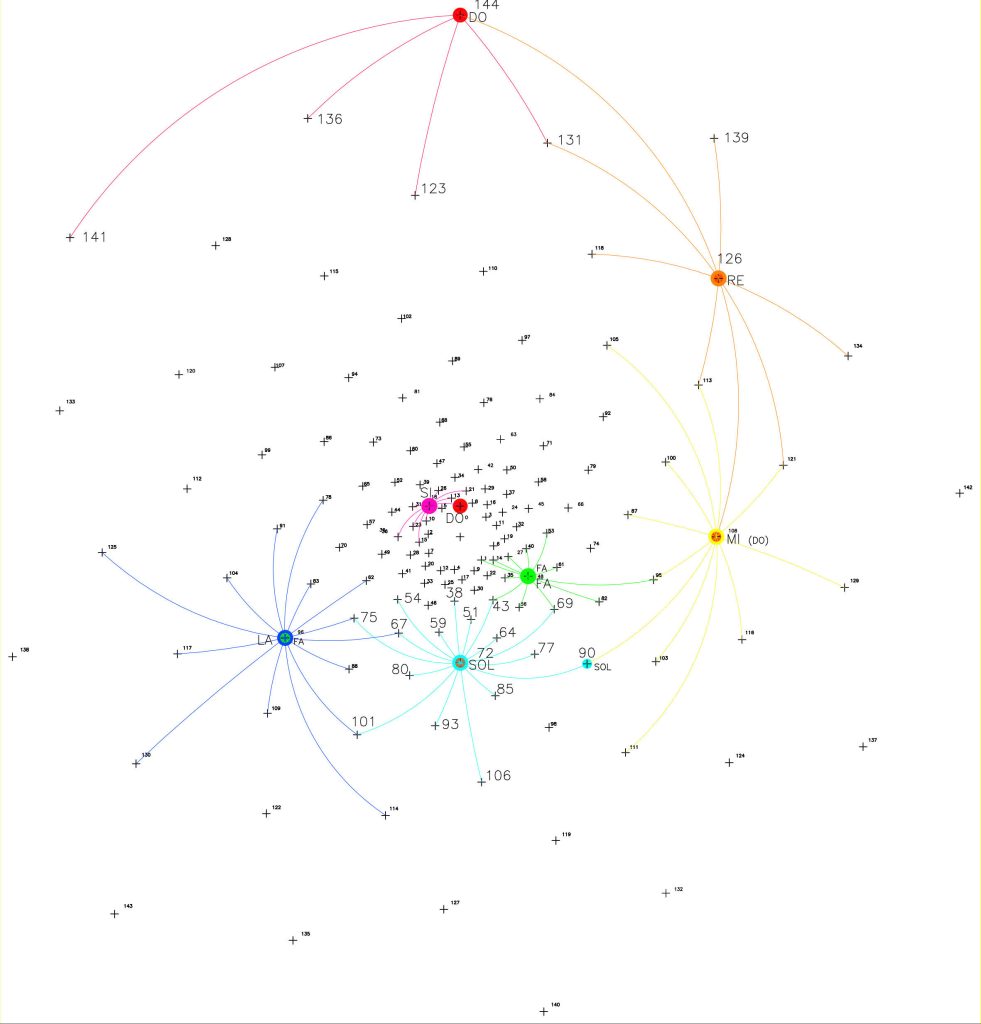
Así por ejemplo, el punto 144, último de la serie, “borde” del sistema y notación musical de DO u OCTAVA tiene como vecinos más próximos a los puntos 136, 131 y 139 y en el siguiente salto, a los puntos 141, 123 y 126. Es decir, las conexiones o el camino entre este punto 144 y sus próximos están indicados por las espirales que acabamos de ver.
Por ejemplo, el p.136 se relaciona con el p. 144 mediante la espiral 1/8; el p. 131 tiene como camino a la espiral 1/13 y por último, la conexión con el p. 139 es la espiral 1/5.
En la siguiente relación del p. 144 está el p.141 mediante la espiral 1/3, el p. 123 mediante la espiral 1/21 y por último, el p.126 se conecta con el borde o p. 144 mediante la espiral 1/18.
Esto es, la conexión entre los diferentes puntos de este entramado espacial esta guiado por las curvaturas espaciales de estas lineas espirales y los puntos significados por las notas actúan como focos de irradiación o centros de confluencia y atracción.
Si observamos de nuevo en la figura 15, el punto 72 correspondiente a la nota SOL (que angularmente tiene una diferencia de 180º con el anterior p. 144) está rodeado de puntos vecinos por todos lados y podemos utilizar este punto o foco como referencia en ese entorno.
De nuevo, las espirales nos marcan el camino, escogiendo los “trozos” de espiral que pasan, en este caso, por esa nota pura. Y surgen “casualidades”: esos “tramos” de espirales, definidas por, justo el punto anterior y posterior, siempre dan el mismo valor numérico: suma de esos puntos contrarios u opuestos. Es decir, la suma del valor de los puntos extremos de esas “curvaturas” cuyo centro es la nota pura, dan siempre el mismo valor numérico, como por ejemplo la nota SOL.
Así la nota Sol, ocupando el p. 72, está a la «mitad» de la octava 1 /1 y 2/1 como relación 3/2 y valor angular de 180º. La espiral 1/34 pasa por este punto 72 siendo su anterior el p.38 y el posterior 106, su suma es 144. La espiral 1/21 pasa por el p.51 y el posterior es el p.93, su suma es 144; la espiral 1/8 pasa por el p. 64 y el posterior es el p.80, su suma 144. 144/2=72 punto numérico de la nota Sol.
Las espirales de potencias de Φ participan en este mismo juego. La espiral 1/29 tiene como punto anterior el p. 43 y el posterior es el p.101, de nuevo su suma es 144. La espiral 1/18 tiene como punto anterior el p. 59 y el posterior es el p. 90, su suma 144. 144/2=72.
También podemos observar que cada nota ha creado como un paraguas o umbral, que califica o colorea una región del plano, o del espacio (puesto que este crecimiento que hacemos en el plano, es una proyección del espacio).
Por la propia estructura de la octava musical (que ya hemos visto en anteriores artículos): una progresión geométrica en base 2, nos encontramos que dentro de la octava existen otras octavas: Así, por ejemplo si la octava tiene como distancia el valor la unidad (Do=1/1 y Octava=2/1), la distancia Sol-Do corresponde a una octava 1/2, la distancia Mi-Sol equivale a una octava 1/4 y la distancia Re-Mi equivale a una octava 1/8. Esto es, dentro de una octava de valor unidad, existen dos octavas de valor 1/2, cuatro octavas de valor 1/4 y ocho octavas de valor 1/8 y por ello, podemos establecer de nuevo, las notas puras correspondientes a estas cuatro tipos de octavas. (4) Fig. 16

En este estudio, mencionaremos dos octavas de 1/8 correspondientes a Do/Re y Re/Mi, una octava de 1/4 de Mi/Sol, otra de 1/2 Sol/Do y la general 1/1 Do/Octava.
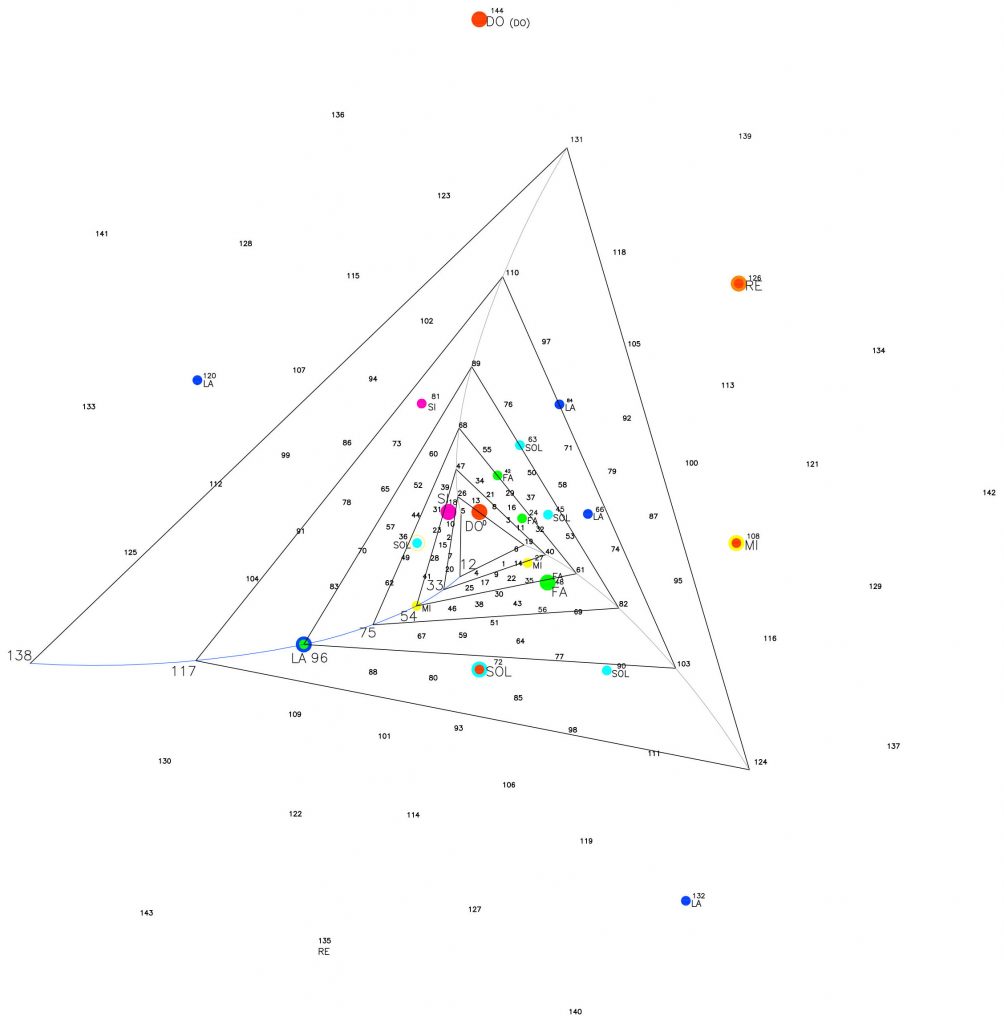
En la figura 17, veremos que entre los ejes que definen el espacio Do-Re (octava de 1/8 definida entre el punto 144 y el punto126) angularmente corresponde a 45º y encontramos, entre ambos ejes, la existencia de tres puntos definidos por las notas Fa, Sol y La unidas por la espiral 1/21.
En el espacio Re (p.126)-Mi (p.108), equivalente a una octava de 1/8, y de valor angular de 45º, también existen esas tres notas puras unidas también por la espiral 1/21 (puntos 24, 45 y 66).
En el espacio Mi (p.108)-Sol (p.72), equivalente a una octava de 1/4 y de valor angular de 90º, ya existe un escalón más: la nota Mi, además de las tres anteriores Fa, Sol, La unidas también por la espiral 1/21 (puntos 27, 48, 69, y 90)…
Sucesivamente van apareciendo notas puras en las diferentes octavas. Es decir, encontramos que no sólo siete puntos se han significado sino que otros más han comenzado a brillar.
Utilizando ese fondo definido por los puntos de crecimiento del nº Φ, podemos definir las espirales que pueden corresponder a la escala sonora de la gama diatónica y tal vez estas geometrías aporten otros aspectos de cada paso o nota en esa continuidad sonora de la escala musical. Fig.18
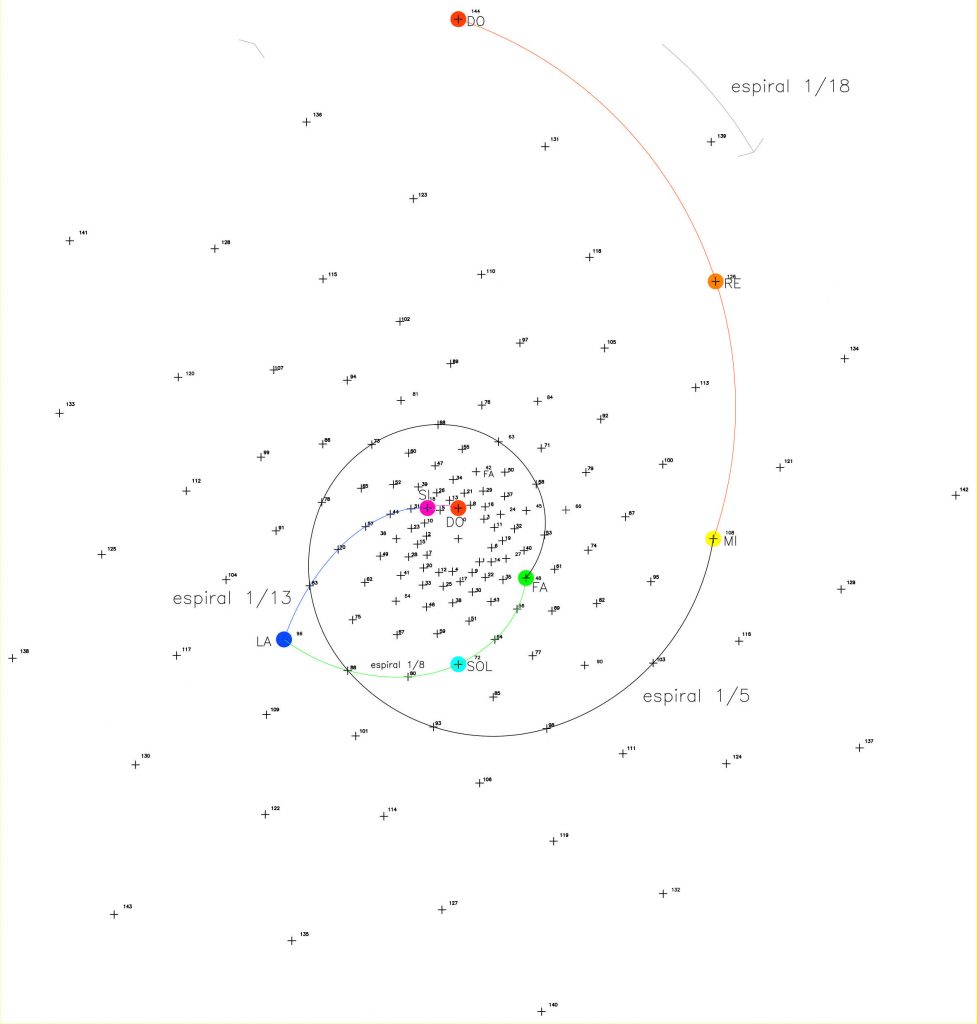
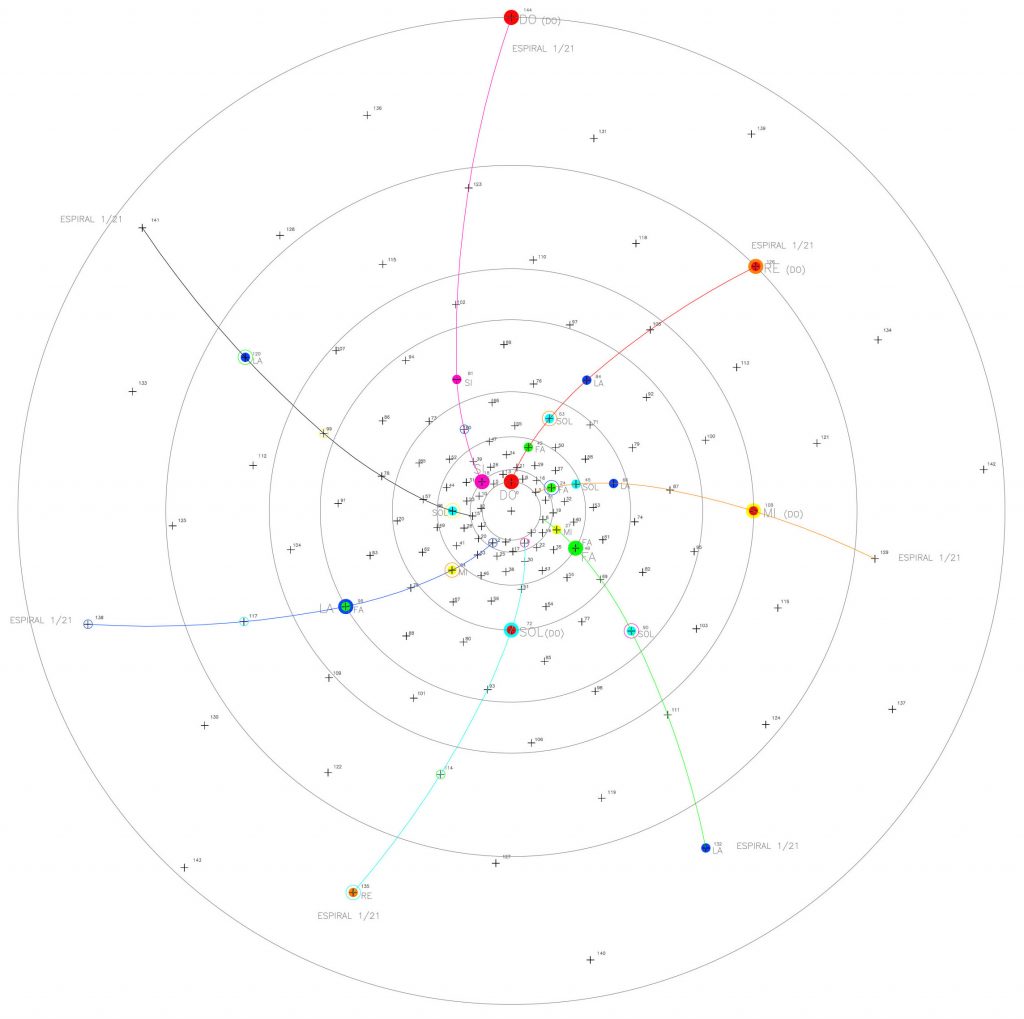
Si partimos del punto 144 como Unísono, la espiral 1/18 une las notas Do o Unísono, Re (p.126) y Mi (p.108), pero también más adelante pasa por la nota Sol (p.72) y luego por la nota Si (p.18) para llegar al Do (p.0). La espiral 1/8 es la misma que la anterior pero de sentido contrario, une las notas Do (p.0), Fa (p.48), Sol (p.72), La (p.96) y vuelve al Do (p.144). Ambas, 1/18 y 1/8 son espirales con una simetría implícita. Por último, la espiral 1/13 une las notas La (p.96) y Si (p.18)…
Esto es, parecería que en este desarrollo espiral, una octava «ascendente» (Do, Re, Mi…), guiada por la espiral 1/18, se interioriza y numéricamente «baja o decrece» desde el p.144, Octava, al punto 0 o Unísono, pasando por Re(p.126), Mi (p.108), Sol (p.72), Si (p.18) hasta Do o punto 0. Y a la vez, una octava «ascendente», guiada por la espiral 1/8, desde el punto 0 o Unísono pasando por Fa(p.48), Sol(p.72), La(p.96) para llegar al p. 144 u Octava y en su recorridos aparecen determinadas notas de las octavas interiores ya mencionadas.
Ahora bien, en la escala musical ascendente, tenemos el salto de Mi a Fa, en la que se produce una retardación en el nº de vibraciones, es decir, el proceso de vibración de la octava diatónica es discontínuo con dos puntos de retardación, el intervalo Mi-Fa y el intervalo Si-Do. Y como podemos ver en la figura 19, ni la espiral 1/8 ni la 1/18 resuelven la continuidad entre las notas Mi y Fa.
Qué espiral tiene capacidad de unir ambas notas?.
Si observamos la figura anterior, podemos ver que la espiral 1/5 nos posibilita ese recorrido. Espiral que nace o acaba, según lo miremos, en el punto 143. Punto definido angularmente por el valor 222,5º o valor angular del nº Φ . Es decir, la espiral 1/5 finalizando en el punto 143 y naciendo en el punto 3, rellena el intervalo Mi-Fa… Podemos decir que una espiral que finaliza justo en el último valor de Φ en la serie angular de 137,5º, rellena el intervalo Mi-Fa…
Recordemos las simetrías implícitas antes mencionadas: este punto final 143, coincide angularmente con el punto 1 del crecimiento lineal de las espirales del φ angular como 222,5º… Así, la simetría implícita entre las espirales 1/8 y 1/18, correspondiendo a dos series diferentes (Fibonacci y Lucas) permiten la conexión entre las notas de la gama a excepción del intervalo Mi-Fa rellenado por una espiral de velocidad más lenta.
En la figura 19 se recogen estas diferentes espirales definidas por las razones 1/8, 1/13 y 1/18 y 1/5 donde cada una de ellas representa una etapa de frecuencias y por ello, una diferente velocidad.
Y así como ya hemos visto en el artículo anterior, el armónico octavo recoge las notas Do, Re, Mi, Sol, Si y Octava de la escala diatónica y el armónico duodécimo las notas Do, Fa, Sol, La y Octava, en el crecimiento angular de valor Φ de 137,5º, la espiral 1/18 interpreta el primer armónico y la espiral 1/8 el segundo armónico citado, y da un dato más: la continuidad en la escala ascendente está en la espiral 1/5 que une ambas notas del intervalo.
3.- ESPIRALES DE RAZÓN 1/7.
Hasta ahora las espirales producidas por el crecimiento angular de 137,5º tanto en su versión «recta» como en su versión «curva» de unión de los puntos, daban una imagen similar para su entendimiento; desde las primeras 1/2, 1/3 y 1/5 donde la curvatura o proximidad de los puntos ayudaban a su comprensión como a las series más amplias 1/21 o 1/34 donde la distancia entre puntos casi las convertían en líneas rectas.
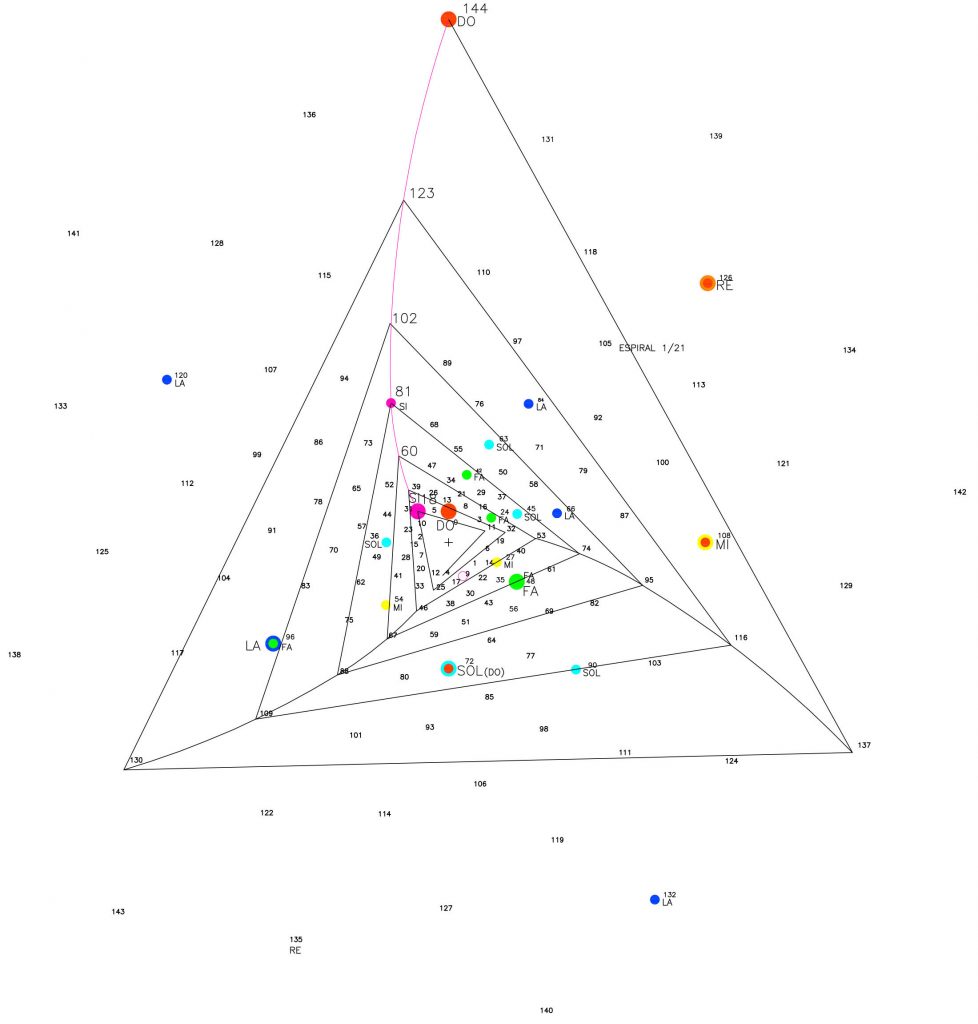
Tal vez de los casos más evidentes de unión por líneas rectas es la serie 1/7 donde el sistema de crecimiento reproduce «triangulaciones» y donde la unión de esos vértices hace surgir siete espirales de razón 1/21 que podemos nombrar como Espirales de las notas de la octava angular.
Empezamos en orden descendente. En la figura 20, la espiral de la Nota Si o relación 15/8, tiene sus límites definidos por la nota Si (p.18) y por la octava o Do (p.144), en su desarrollo otro punto característico es p.81 que define la nota Si de la octava interior Sib-Do (recordemos la Fig.16 y el concepto de octavas dentro de octavas).
La reducción de los puntos a los nueve primeros números de esta razón 1/21 produce la secuencia numérica: 18/39/60/81/102/123/144 a 9/3/6/9/3/6/9.
La siguiente espiral corresponde a la nota Sib o relación 7/4. Fig.21. Comienza en el p.15 y finaliza en el p.141. En su recorrido aparecen otros puntos significados por notas de octavas interiores como ya hemos explicado. De nuevo, la reducción numérica permite fijar el ritmo de esta espiral en 6/9/3/6/9/3
La espiral de la nota La o relación 5/3, Fig. 22, comienza en el punto 12 reproduciendo la secuencia 12/ 33/ 54/ 75/ 96 o nota La/ 117/ 138 y de nuevo, la reducción permite definir el ritmo en 3/ 6/ 9/ 3/ 6/ 9/ 3. En su recorrido se han significado también los puntos 54 y 96 de notas de octavas interiores.
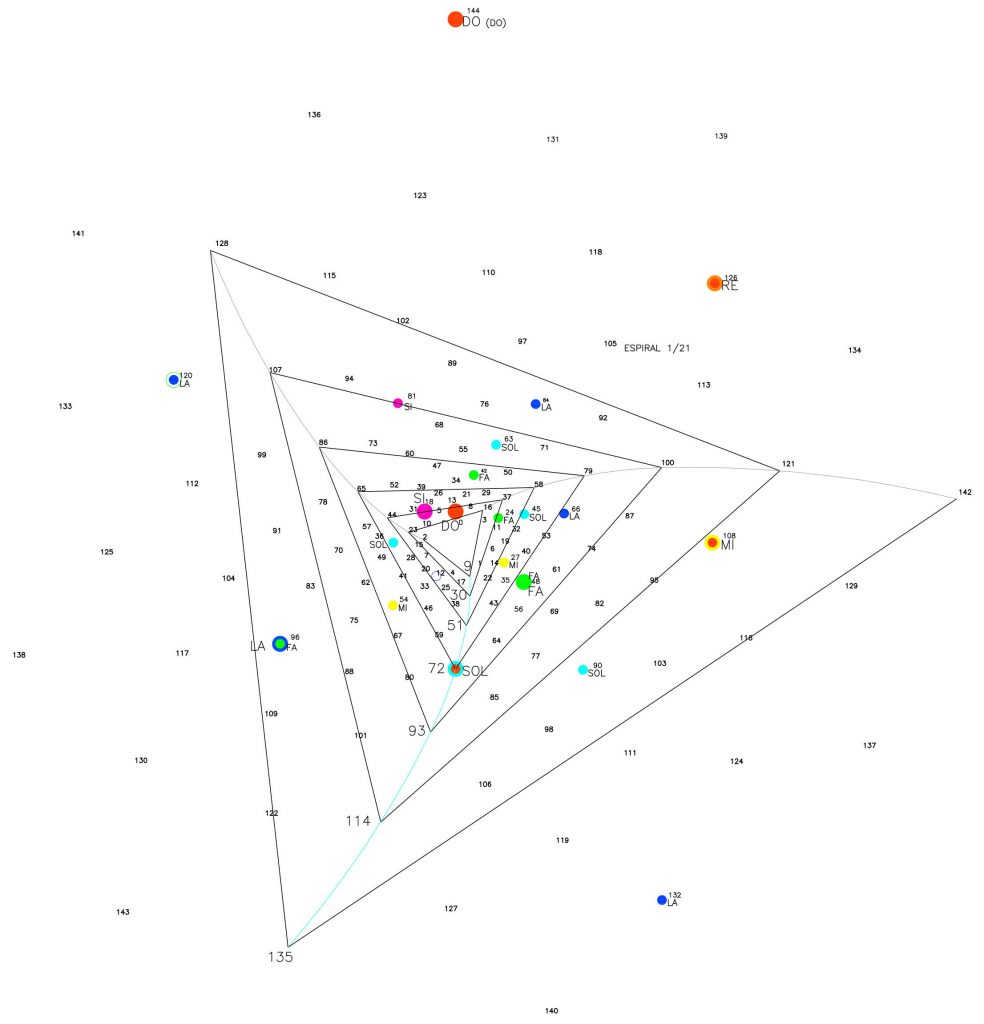
La espiral de la nota Sol o relación 3/2, Fig. 23, comienza en el punto 9 o nota Si de la octava interior (Mi/Sol) siguiendo la secuencia 30/ 51/ 72 (nota Sol)/ 93/ 114/ 135 (nota Re de la octava interior (Sol/Do). De nuevo la secuencia numérica de esta espiral es 9/ 3/ 6/ 9/ 3/ 6/ 9.
Ya podemos comprobar en las espirales anteriores esa alternancia en el comienzo de la numeración pero siempre ese ritmo fijado por la triada 3/ 6/ 9.
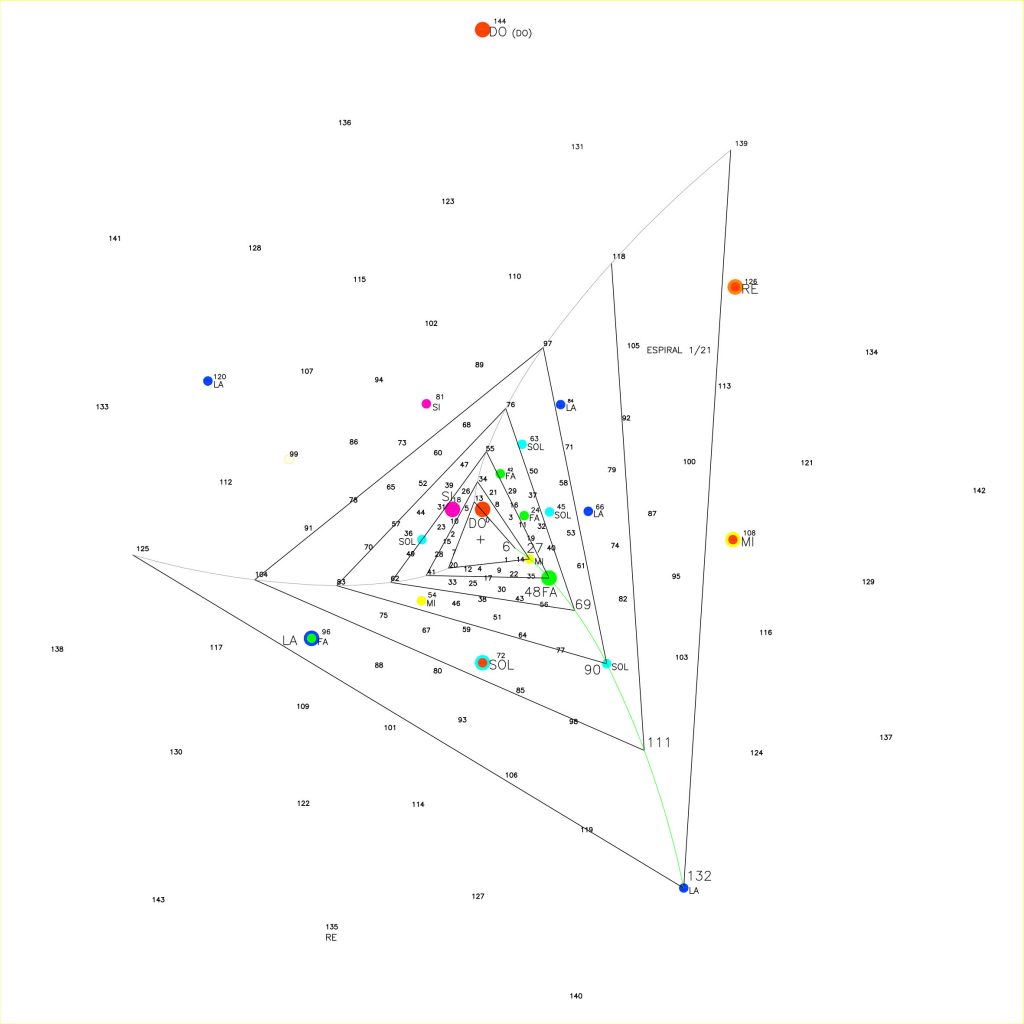
La espiral de la nota Fa o relación 4/3, Fig. 24, comienza en el punto 6 siguiendo por los puntos 27/ 48 / 69/ 90/ 111/ 132; en este caso los puntos 27, 48, 90 y 132 corresponden a las notas Mi, Fa, Sol y La de la octava interior Mi/Sol. La reducción numérica permite afirmar el ritmo de esta espiral en 6 / 9/ 3/ 6/ 9/ 3/ 6.
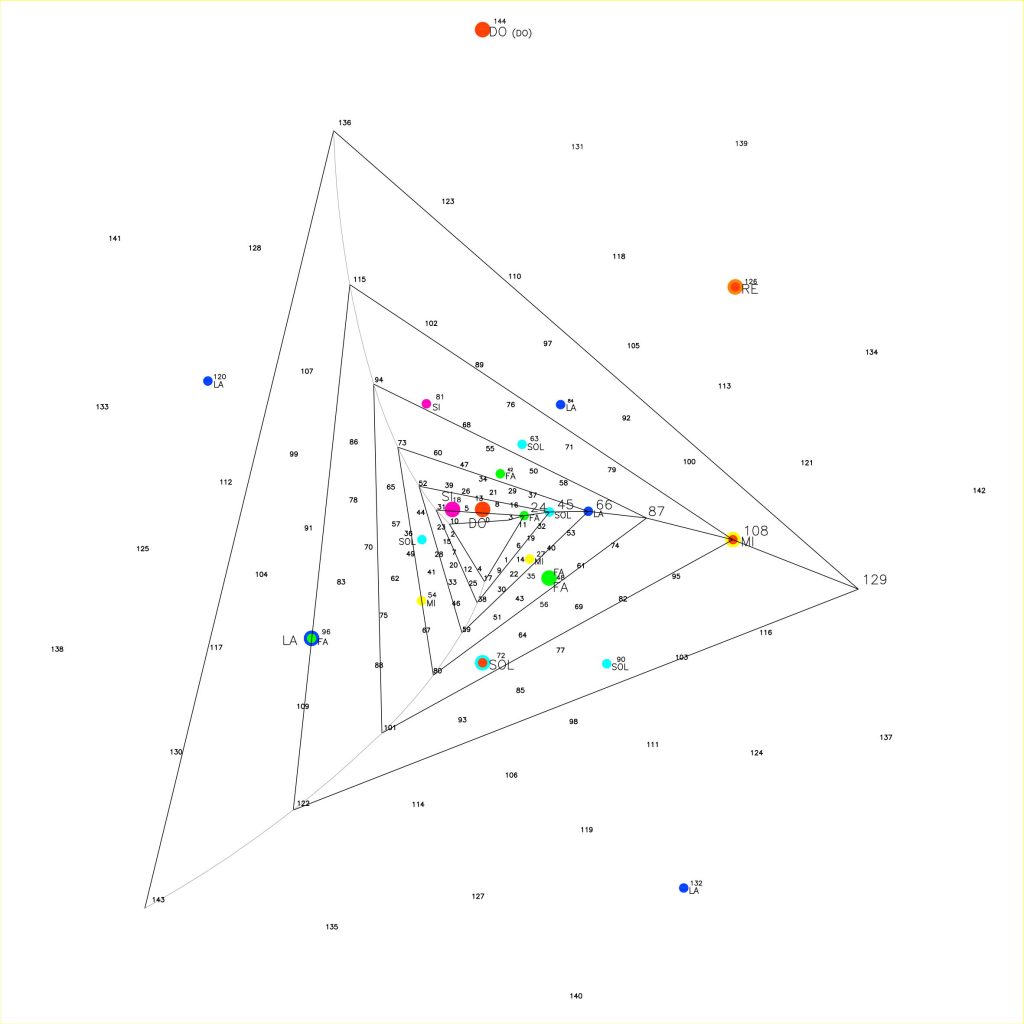
La espiral de la nota Mi o relación 5/4, Fig. 25, comienza en el punto 3 siguiendo el ritmo de 24/ 45/ 66/ 87/ 108/ 129 donde los puntos 45 y 66 reproducen notas de octavas interiores. El ritmo en este caso, es de 6/ 9/ 3/ 6/ 9/ 3/ 6.
Por último, la espiral de la nota Re o relación 9/8, Fig. 26, corresponden a la unión de los vértices 0/ 21/ 42/ 63/ 84/ 105 /129 reproduciendo la secuencia 3/ 6/ 9/ 3/ 6/ 9. En este caso, los puntos 42, 63 y 84 corresponden a las notas puras Fa, Sol y La de la octava interior Do/Re.
Esto es, hay siete espirales de razón 1/21 que en sus recorridos, pasan por puntos definidos «coloreados» por frecuencias concretas definidas por notas musicales.
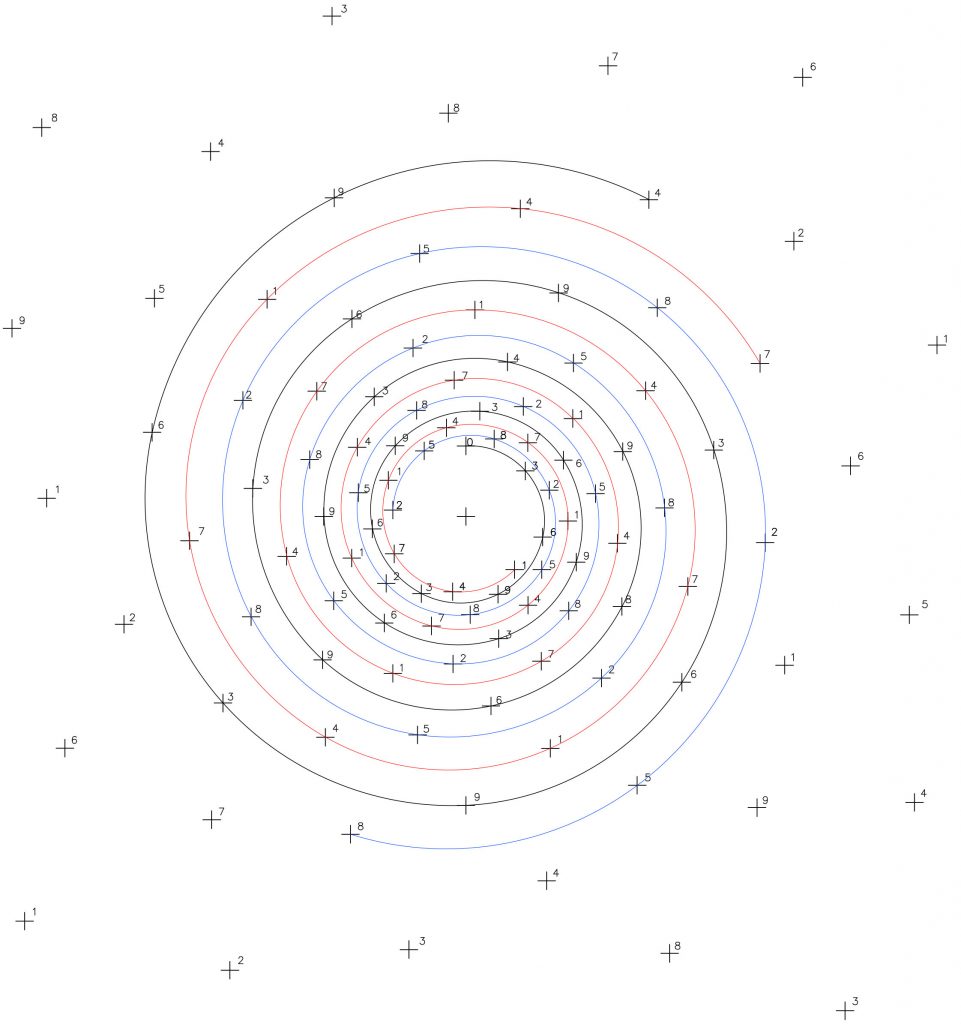
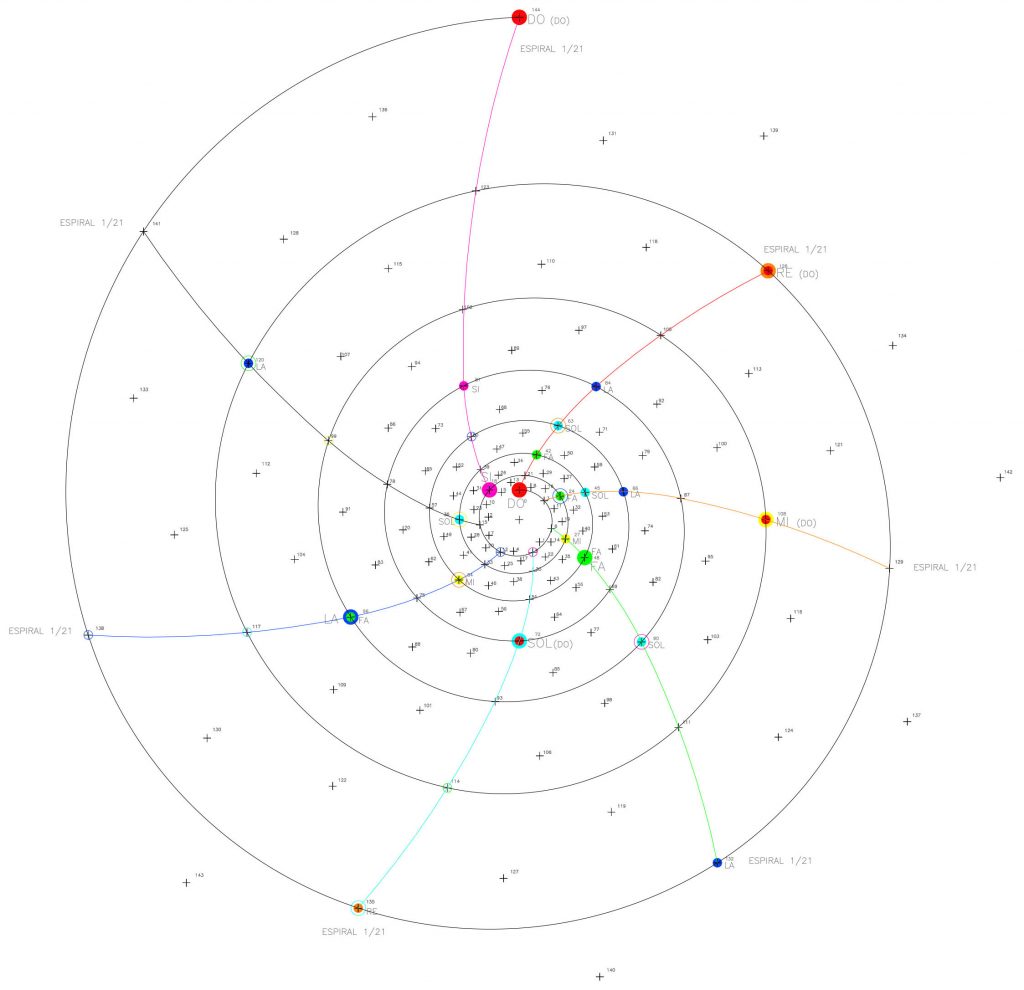
Y con esto, llegamos al final de este apartado con la figura 27 sintetizando este proceso. En la imagen, siete círculos concéntricos recogen las notas angulares de la octava diatónica y la siete espirales de razón 1/21 que acabamos de ver cuya ritmo está marcado por la triada 3/6/9…(cuyo orden numérico va alternandose), indican los puntos significados «musicalmente» del proceso.
4.-VALOR DE LOS SECTORES.
Hasta ahora todo lo que hemos ido exponiendo se ha referido a las líneas o espirales que conectan los diferentes puntos del escenario espacial concreto que califica el nº φ.
Formas lineales de gran belleza que al superponerse, resultan en formas planares; planos cuya sectorización resulta de la superposición de, al menos, dos espirales. Y así como hemos visto, la existencia de ciclos y ritmos en las propias espirales, vamos a revisar qué sucede al estudiar el «valor» de los esos sectores cuadrangulares cuyo dibujo recuerda a la organización de los pétalos de las flores.
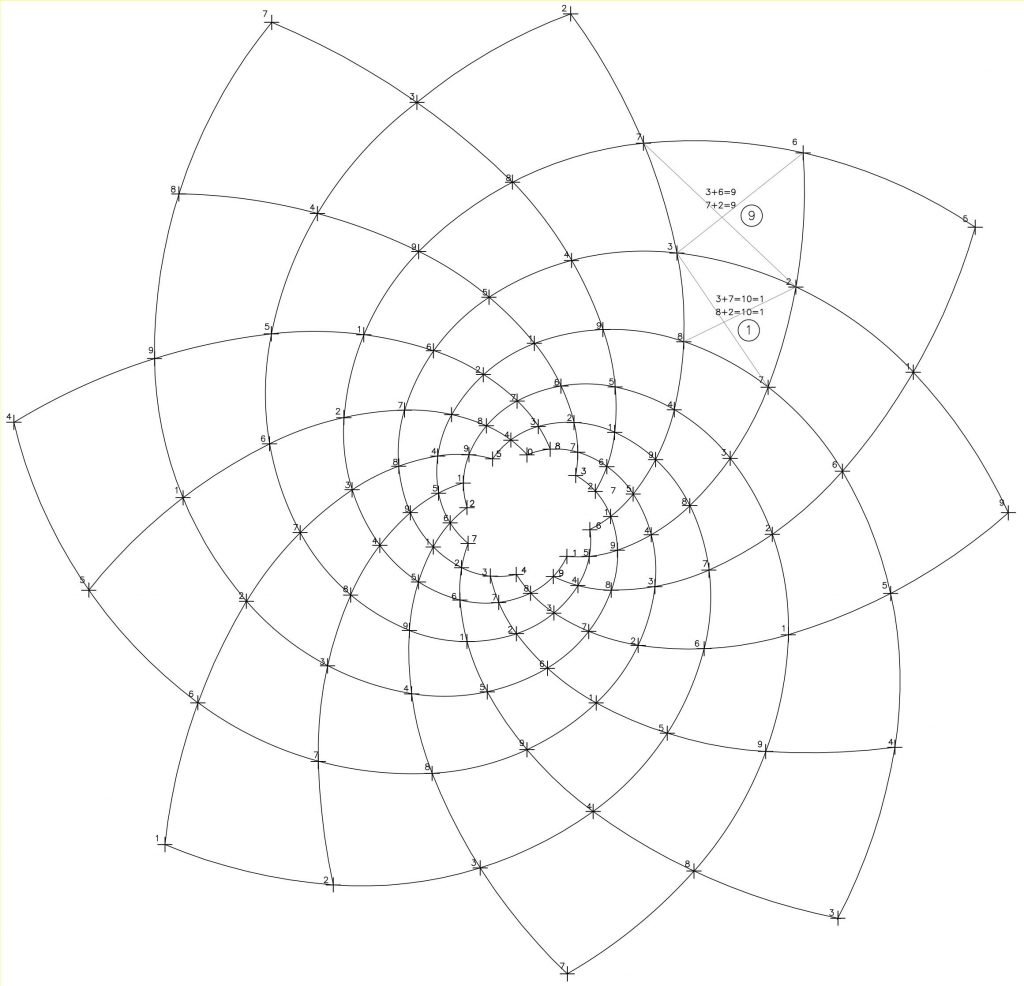
Seguiremos el proceso mediante la figura 28: superposición de las espirales de razón 1/8 y 1/13, ampliando parcialmente su ciclo completo y aplicando la reducción numérica a los nueve primeros números.
Recordemos que en cada espiral 1/8, los puntos siguen la secuencia numérica 1/2/3/4/5/6/7… y cada espiral 1/13 reproduce un ritmo basado en el 4; así, si empezamos por el punto 4, la serie queda definida por 4/8/3/7/2/6/1/5/9 (4+4=8, 8+4=12=3, 7=3+4, 7+4=11=2…)
Tomemos el sector cuadrangular definido por los vértices 3, 6, 2, 7 de la figura 28; la suma de los vértices opuestos da el mismo valor 9. El siguiente con el mismo criterio da el valor 1, y así sucesivamente.
La figura 29 es una imagen con todos los sectores definidos por un «valor» numérico. Los «valores» de los sectores de las bandas dextrógiras siguen un secuencia basada en los números impares seguidos de los pares 1/3/5/7/9/2/4/6/8 y los «valores» de los sectores de las bandas levógiras siguen la secuencia numérica 1/2/3/4/5/6/7/8/9…
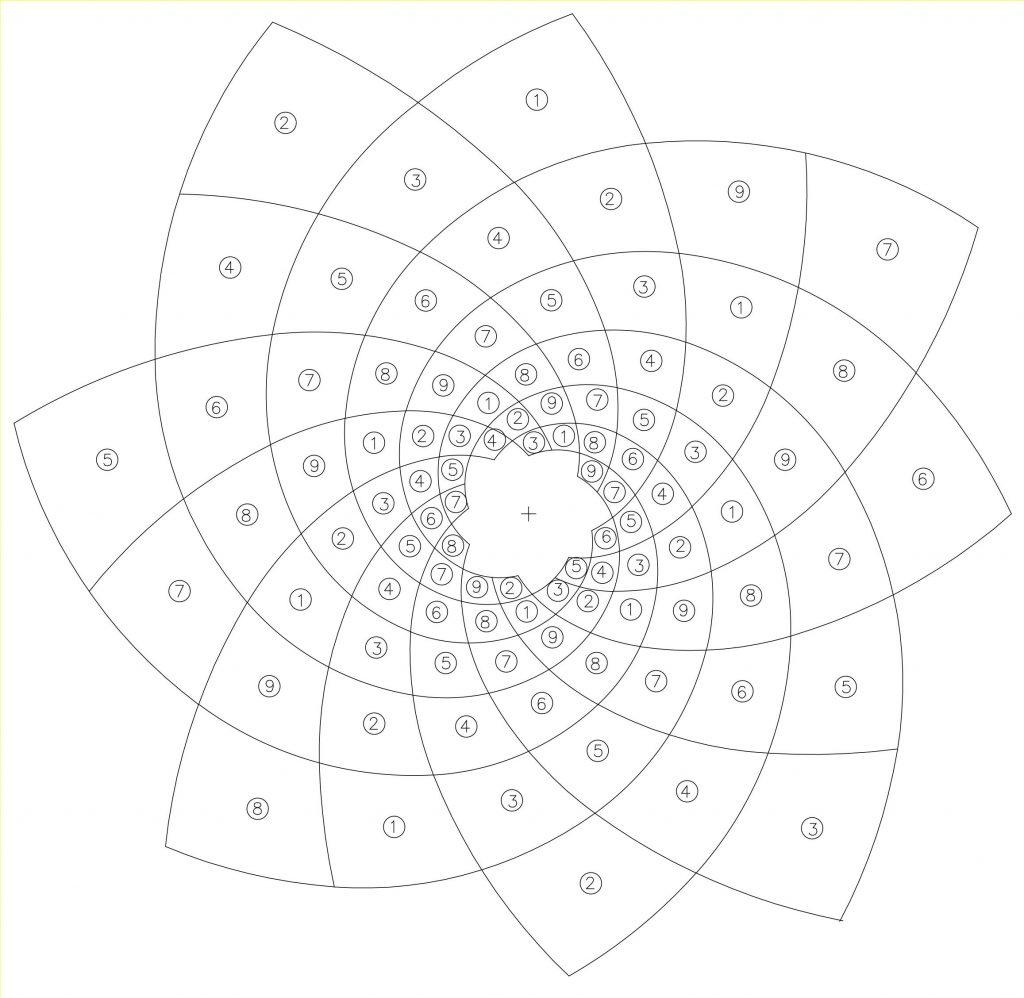
En ese mundo curvo que contiene infinitas direcciones espaciales y de sentidos opuestos, es fácil orientarse siguiendo las secuencias numéricas intrínsecas al proceso de su formalización. Una imagen sintética que expresa de manera sencilla los ritmos subyacentes que existen en estos procesos de expansión y crecimiento; un paso en la profundización de la misma figura 28.
5.- IZQUIERDA Y DERECHA.
Y siguiendo con los ritmos y patrones, un último apunte… (5)
Podemos trazar un eje vertical sobre la Fig.1 del comienzo que una los puntos 0 y 144. El hecho de su trazado ya marca el escenario completo diferenciado entre el lado izquierdo (I) y el derecho (D) y por ello, todos los puntos toman una posición. Fig.30.
Así en la primera vuelta de 360º se significan tres puntos (0, 1, 2):
0) 0º
1) 137,5º (D)
2) 137,5º+137,5º=275º (I)
En la segunda vuelta se significan tres puntos (3, 4, 5):
3) 52,5º (D)
4) 190º (I)
5) 327,5º (I)
En la tercera vuelta, se significan dos puntos (6, 7):
6) 105º (D)
7) 242,5º (I)
En la cuarta vuelta, se significan tres puntos (8, 9, 10):
8) 20º (D)
9) 157,5º (D)
10) 295º (I)
En la quinta vuelta, se significan tres puntos (11, 12, 13):
11) 72,5º (D)
12)210º (I)
13) 347,5º (I)
En la sexta vuelta, se significan dos puntos ( 14, 15):
14) 125º (D)
15) 262,5º (I)
Y así sucesivamente hasta llegar a la vuelta 55. (6)
Si revisamos las 55 vueltas, comprobaremos que las únicas posibilidades de combinación son:
DI= A
DDI=B
DII=C
y por ello, el sistema de crecimiento se ordena como:

La octava diatónica está formada por tres intervalos definidos por
Tono mayor=9/8=A
Tono menor=10/9=B
Semitono diatónico=16/15=C
Establecemos las notas y los intervalos entre ellas; así entre Do-Re, Fa-Sol y La-Si funciona el tono mayor, entre Re-Mi y Sol-La es el tono menor y entre Mi-Fa y Si-Do el semitono.

Se produce un ritmo idéntico entre las siete primeras vueltas y la gama diatónica con su comienzo en modo LA.
Ordenando todas las vueltas realizadas:
1 2 3 4 5 6 7 8 9 10 11 12 13
A C A B C A B A B C A B C
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
A C A B C A B A B C A B C A A
29 30 31 32 33 34 35 36 37 38 39 40 41
A B C A B C A C A B C A B
42 43 44 45 46 47 48 49 50 51 52 53 54 55
A B C A B C A C A B C A B A
Esta coincidencia entre la disposición de los puntos definidos por la razón aúrea angular de 137,5º y el orden de los tonos de la octava diatónica parece indicar la existencia de un orden subyacente entre tanta aparente diversidad… (6)
Algo así como que al comenzar Φ su movimiento angular de 137,5º reproduce un orden sucesivo que podemos establecer como:
– 7 intervalos seguidos en modo LA
– 3 primeros intervalos de la gama (A B C)
– 3 primeros intervalos de la gama (ABC)
– 7 intervalos seguidos en modo LA
– 3 primeros intervalos de la gama (ABC)
– 3 primeros intervalos de la gama (ABC)
– 1 el primer intervalo (finaliza en la vuelta 27)
………………………………………………………………
– 1 el primer intervalo (A) (comienza en la vuelta 28)
– 3 primeros intervalos de la gama (ABC)
– 3 primeros intervalos de la gama (ABC)
– 7 intervalos seguidos en modo LA
– 3 primeros intervalos de la gama (ABC)
– 3 primeros intervalos de la gama (ABC)
– 7 intervalos seguidos en modo LA
para volver en la vuelta 55 y completar el ciclo.
Una simetría subyacente en ese movimiento expansivo de creación donde se repite el 1, el 3 y el 7…
Y viene al recuerdo el conocimiento de la Tradición Antigua (ya desarrollado en otros artículos) que habla de tres leyes en la creación: la ley del Uno, la ley del Tres o triada y la ley del Siete u octava.
«La ley del Uno define el origen y centro de la creación: en el principio es el Uno, en el desarrollo es Uno y en la disolución es Uno.
La ley de Tres o triada define el acto de la creación. Esto es, para que un hecho, suceso o acontecimiento se manifieste es necesaria la concurrencia de tres cualidades, elementos o fuerzas.
La ley de Siete u octava define la creación en el tiempo. Esto es, la ley que rige el conjunto de acon–tecimientos que la ley de la triada pone de manifiesto, la ley que define su sucesión en el tiempo es llamada ley de la octava.
Dice la Tradición Antigua que son diferentes niveles de conocimiento y experiencia que implican directamente a los conceptos de espacio y tiempo. En la ley del Uno , necesariamente no existe el espacio ni el tiempo. En la ley del Tres se origina el espacio y en la ley del Siete se origina el tiempo. Por ello, para llegar al Uno hay que trascender el espacio y el tiempo».
Recordemos la imagen de la figura 27; siete círculos concéntricos y siete espirales de razón 1/21 sintetizan junto a la espiral 1/3, esa conexión entre el escenario espacial regido por la razón angular φ y las cualidades inherentes a la gama de sonidos o frecuencias. Fig.31
También recordemos que en esa escala de frecuencias, el nº φ ocupa el lugar del Sol# (relación 8/5 de la serie Fibonacci).
Parece que mediante una observación más detenida sobre el nº Φ y su relación con la octava, se ponen de manifiesto casualidades y coincidencias, simetrías, ritmos y patrones que sugieren la existencia de órdenes y leyes eternas no visibles en apariencia.
Así, podríamos decir que:
Tanto en un tablero de juego ordenado por una geometría Φ, como en un escenario que vibra con una frecuencia correspondiente a un Sol#, ambas dimensiones expresan el mismo patrón creativo
En los próximos artículos, examinaremos los siguientes números geométricos.
Notas:
1.- The Hidden Geometry of Flowers. Keith Critchlow. Floris Book. 2011
2.-Vistas parciales de las espirales 1/13 y 1/29 en su reducción numérica en las F12 y F13.
3.- Recordar el final del artículo anterior en la definición de la octava angular. En el punto 6 están recogidos las
55 vueltas y los 144 puntos que definen el ciclo angular del nº Φ.
4.- Podemos establecer que:
– en la octava interior DO (p.0)/RE( p.126) existen las notas puras Fa (p.42, Sol (p.63), La (p.84).
– en la octava RE (p.126)- MI (p.108) existen las notas puras Fa (p.24), Sol (p.45), La (p.66)
– en la octava MI (p.108)- SOL (p.72) existen las notas puras Mi (p.27), Fa (p.48), Sol (p.90), La (p.132).
– en la octava Sol (p.72)- DO (p.144) existen las notas puras Mi (p.54), Fa (p.96), Sol (p.36), La (p.120), Si (p.81).
5.- Todo lo que ahora se está exponiendo fue investigado y desarrollado en la década de los años 90 del siglo pasado especialmente la relación entre el nº Φ y la octava. En este 2023, se han revisado y actualizado dicha investigación con nuevos datos.
Si consideramos la octava como la ley del siete que fija u ordena los acontecimientos en el tiempo siempre podemos definir ese tiempo (cualquiera sea la cantidad) como longitud temporal de valor unidad, y considerar los pasos de la octava como etapas de un proceso (tiempo) que ha tenido un comienzo y un final.
Entre la información que en ese tiempo llegó a mis manos, he de mencionar unas fotocopias de unos dibujos en inglés, sobre Φ que debieron formar parte de una conferencia impartida en Londres en la sede de la Economics Science School, posiblemente por algún miembro o autor desconocido. En ellas, aparecía esta idea de «izquierda y derecha del cosmos», ese ritmo y orden en la «atmósfera» del número Φ, que de alguna manera, apuntaba y ampliaba las ideas que en ese tiempo estaba desarrollando.
Así, nos encontramos que el valor de Φ como la relación de 8/5 de la serie Fibonacci es considerada en Música, como la Sexta menor ocupando ese lugar entre Sol y La y actuando como un SOL#. Así mismo, el valor de Φ1/2 podría ocupar ese rango entre Mi y Fa. Otro dato a considerar pues en el artículo ya mencionado de «la octava y la vivencia del tiempo» hablamos de las cualidades asociadas a las notas y la triada de Φ1/2, Φ1/1, Φ3/2.
6.- Definición de las vueltas y puntos de la serie angular 137,5º
7 vuelta: 16) 40º (D)/17) 177,5º (D)/18) 315º (I)
8 vuelta:19) 92,5º (D)/20) 230ª (I)
9 vuelta: 21) 7,5º (D)/22) 145º (D)/23) 282,5º (I)
10 vuelta: 24) 60º (D)/25) 197,5º (I)/26) 335º (I)
11 vuelta: 27) 112,5º (D)/28) 250º (I)
12 vuelta: 29) 27,5º (D)/30) 165º (D)/31) 302,5º (I)
13 vuelta: 32) 80º (D)/33) 217,5º (I)/34) 355º (I)
14 vuelta: 35) 132,5º (D)/36) 270º (I)
15 vuelta: 37) 47,5º (D)/38) 185º (I)/39) 322,5 º (I)
16 vuelta: 40) 100º (D)/41) 237,5º (I)
17 vuelta: 42) 15º (D)/43) 152,5º (D)/44) 290º (I)
18 vuelta: 45) 67,5 º (D)/46) 205º (I)/47) 342,5º (I)
19 vuelta: 48) 120º (D)/49) 257,5º (I)
20 vuelta: 50) 35º (D)/51) 172,5º (D)/52) 310º (I)
21 vuelta: 53) 87,5º (D)/54) 225º (I)
22 vueltas: 55) 2,5º (D)/56) 140º (D)/57) 277,5º (I)
23 vuelta: 58) 55º (D)/59) 192,5º (I)/60) 330º (I)
24 vuelta: 61) 107,5º (D)/62) 245º (I)
25 vuelta: 63) 22,5º (D)/64) 160º (D)/65) 297,5º (I)
26 vuelta: 66) 75º (D)/67) 212,5º (I)/68) 350º (I)
27 vuelta: 69) 127,5º (D)/70) 265º (I)
28 vuelta: 71) 42,5º (D)/72) 180º-/73) 317,5º (I)
29 vuelta: 74) 95º (D)/75) 232,5º (I)
30 vuelta: 76) 10º (D)/77) 147,5º (D)/78) 285º (I)
31 vuelta: 79) 62,5º (D)/80) 200º (I)/81) 337,5º (I)
32 vuelta: 82) 115º (D)/83) 252,5º (I)/
33 vuelta: 84) 30º (D)/85) 167,5º (D)/86) 305º (I)
34 vuelta: 87) 82,5º (D)/88) 220º (I)/89) 357,5º (I)
35 vuelta: 90) 135º (D)/91) 272,5º (I)
36 vuelta: 92) 50º (D)/93) 187,5º (I)/94) 325º (I)
37 vuelta: 95) 102,5º (D)/96) 240º (I)
38 vuelta: 97) 17,5º (D)/98) 155º (D)/99) 292,5º (I)
39 vuelta: 100) 70º (D)/101) 207,5º (I)/102) 345º (I)
40 vuelta: 103) 122,5º (D)/104) 260º (I)
41 vuelta: 105) 37,5º (D)/106) 175º (D)/107) 312,5º (I)
42 vuelta: 108) 90º (D)/109) 227,5º (I)
43 vuelta: 110) 5º (D)/111) 142,5º (D)/112) 280º (I)
44 vuelta: 113) 57,5º (D)/114) 195º (I)/115) 332,5º (I)
45 vuelta: 116) 110º (D)/117) 247,5º (I)
46 vuelta: 118) 25º (D)/119) 162,5º (D)/120) 300º (I)
47 vuelta: 121) 77,5º (D)/122) 215º (I)/123) 352,5º (I)
48 vuelta: 124) 130º (D)/125) 267,5º (I)
49 vuelta: 126) 45º (D)/127) 182,5º (I)/128) 320º (I)
50 vuelta: 129) 97,5º (D)/130) 235º (I)
51 vuelta:131) 12,5º (D)/132) 150º (D)/133) 287,5º (I)
52 vuelta: 134) 65º (D)/135) 202,5º (I)/136) 340º (I)
53 vuelta: 137) 117,5º (D)/138) 255º (I)
54 vuelta: 139) 32,5 º (D)/140) 70º (D)/141) 307,5º (I)
55 vuelta: 142) 85º (D)/143) 22,5º (I)/144) 360º –


Dejar un comentario