Anotaciones a otra geometría de la proporción y la armonía. Parte 4

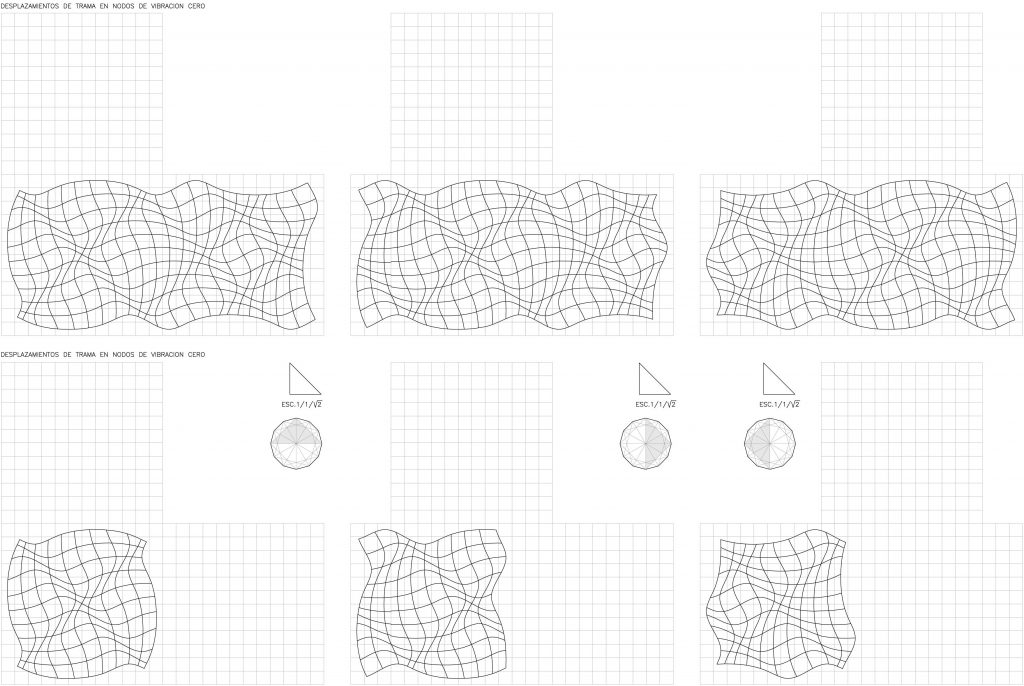
Una forma de percibir la movilidad de las membranas, es mediante sus desplazamientos. En este caso, hemos utilizando el segundo criterio de superposición de la semilla-membrana generada por la escuadra. Fig.32

En los dibujos inferiores de la figura 32 puede verse a la izquierda, la semilla-membrana generada por la escuadra con la posición del ángulo recto en la posición 1/1y en la parte superior, su extensión horizontal. El primer desplazamiento es un giro de 90º en la posición del ángulo recto: un desplazamiento de tres nodos y la posición 5/4 para el ángulo recto; en la parte superior, la misma membrana desplazada tres instantes de tiempo. El segundo desplazamiento es un de giro de 270º en la posición del ángulo recto: un desplazamiento de nueve nodos desde el origen y la posición 7/4 para el ángulo recto. Arriba de nuevo, la misma membrana desplazada nueve instantes de tiempo. Esto es, en la parte superior del dibujo, la misma membrana en tres instantes de tiempo; en la parte inferior: sus tres instantes de comienzo.

O dicho de otro modo, tres energías potenciales de comienzo de la misma membrana.

Y aunque estamos exponiendo el caso de la escuadra, podemos afirmar que los desplazamientos de cada membrana generada por cada triángulo constitutivo del dodecágono ponen en evidencia la importancia del tiempo o la unidad entre espacio y tiempo: el “aquí-ahora” de cada creación. El “ahora” comienzo define la “forma geométrica” de la membrana o su propia “energía potencial”. Esto es, Energía, Forma y Geometría quedan fijadas en el “Ahora” o instante de comienzo…

A.Schönberg, poéticamente, sintetiza este proceso:

“Y por tanto sucede que en su desarrollo, ningún instante es igual a otro. Cada etapa sirve al mismo tiempo de preparación para la próxima. Es una eterna transformación, un crecimiento ininterrumpido de nuevos brotes de la misma semilla. Está claro entonces por qué dos puntos ampliamente separados en este desarrollo son tan distintos y distantes entre sí. De tal manera que, en principio, no reconocemos su relación como conjunto. Únicamente, después de un estudio más acabado, percibimos en la potencialidad del primer periodo la certidumbre del segundo” ₂₄.

Antes de seguir, conviene hacer una pequeña recapitulación. Comenzamos planteando la posibilidad de revisar los conceptos de geometría, proporción y armonía a la luz de las nuevas teorías físicas y las nuevas realidades del espacio tiempo que implican.

Y parece que ahora, a comienzos del siglo XXI, todos los adelantos y descubrimientos que desde mediados del siglo XIX y todo el siglo XX, se han ido realizando y que han afectado de lleno a la comprensión del espacio tiempo, no han rozado siquiera a determinados conceptos que la arquitectura utiliza. Al quedarse de alguna manera, “inútiles o rezagados” de la cultura existente, el sólo hecho de mencionarlos, puede entenderse como fruto de un interés meramente erudito; han pasado de ser conceptos esenciales a accidentales. Pero lo que estamos planteando sobre proporción y armonía está en la base de estos conceptos, es comenzar por el principio, cuando se definieron los conceptos de proporción y armonía y su instrumento fue el monocordio o sistema de oscilación de una cuerda.

Las etapas que hemos recorrido son:

• Una cuerda, en cualquiera que sea su modo de vibración armónica, puede convertirse en la longitud de una circunferencia. Dicha longitud queda pautada por los nodos del modo de vibración. La unión de éstos da origen a un polígono. Este puede descomponerse en sus triángulos constitutivos.
• Cada triángulo constitutivo de cada polígono, genera en su movimiento dextrógiro sobre cada vértice del polígono, una geometría de construcción característica inscrita en la circunferencia cuya longitud define la longitud de la cuerda.
• Esta longitud puede convertirse en tantas cuerdas como número de triángulos contenga el polígono. En cada caso, el modo de vibración de las cuerdas están pautadas por la posición de los vértices de los triángulos, dando tantas “formas de onda” de curvatura variable como posiciones tiene el triángulo.
• Estableciendo una retícula cuyo nº de divisiones corresponde al modo de vibración o al nº de lados del polígono, podemos ir colocando las diferentes “formas de onda” en su orden correspondiente de generación y el conjunto da origen a un plano ondulado.
• Estas retículas de “formas de onda” pueden superponerse o entrecruzarse, según criterios establecidos, manteniendo las simetrías básicas de cada polígono y el resultado ha sido una gran variedad de membranas vibrantes.

Dualidad onda-partícula: polígono y retícula ondulatoria. Dos formas de conocer y también hay que decirlo de comportarse: una cosa es lo que conocemos en la geometría euclidiana y otra su forma de vibración. Y tal vez, tendríamos que recordar las palabras de Roger Penrose ₂₅: ¿Qué es la realidad? Y añadir: ¿Es lo que percibimos? O ¿esto es sólo el aspecto fenomenológico de la realidad?… Aunque tendríamos que aclarar que en las teorías cuántica y de la relatividad general, realmente no existe este dualismo, es más una convención del lenguaje…. Según Einstein, la masa no se transforma en energía. Donde hay masa, hay energía. Donde hay partícula, hay campo….

Retomemos las dos semillas-membranas correspondientes a la escuadra según los dos criterios de superposición para estudiarlas según los puntos característicos que definen la amplitud de la onda: la cresta, el nodo y el valle. Fig.33 y 34

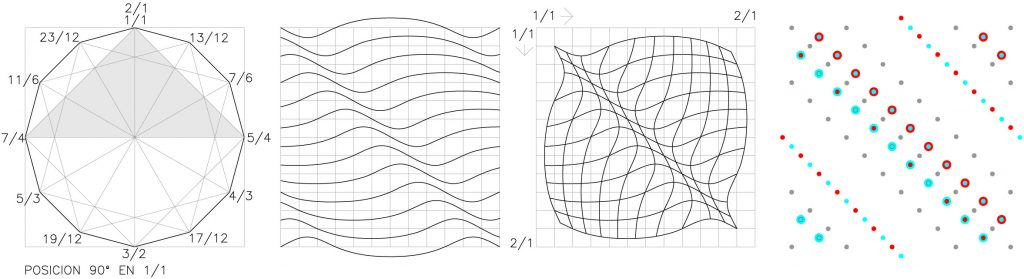
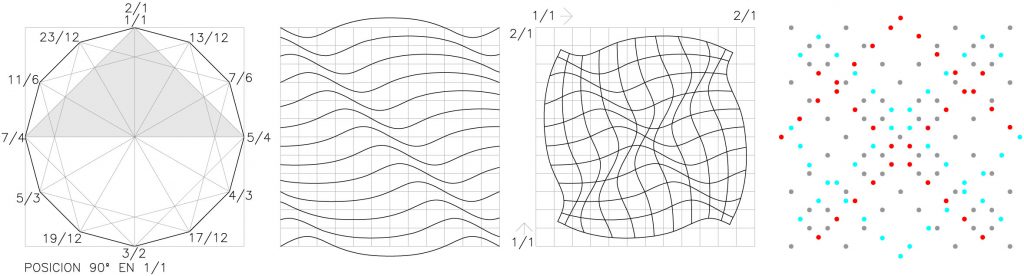
Ambas figuras contienen la construcción geométrica del dodecágono según la escuadra, al lado su retícula de “formas de onda”. A continuación la membrana resultante según cada criterio de superposición y por último, las dos matrices de puntos.

Esto es, de la representación del polígono a su representación como retícula de curvas de frecuencia; de la representación de la membrana a su representación como matriz “pixelada” ₂₆. De la representación en el plano a su representación en el espacio.

Si tomamos la semilla-membrana de la figura 33, la extendemos, seleccionamos el cuadrado central y lo giramos 45º y extraemos la membrana resultante y su matriz de puntos, parecería que este giro o este cambio de visión de la misma membrana, nos ha aproximado a una visión más habitual de la arquitectura en su definición del espacio. Fig.35

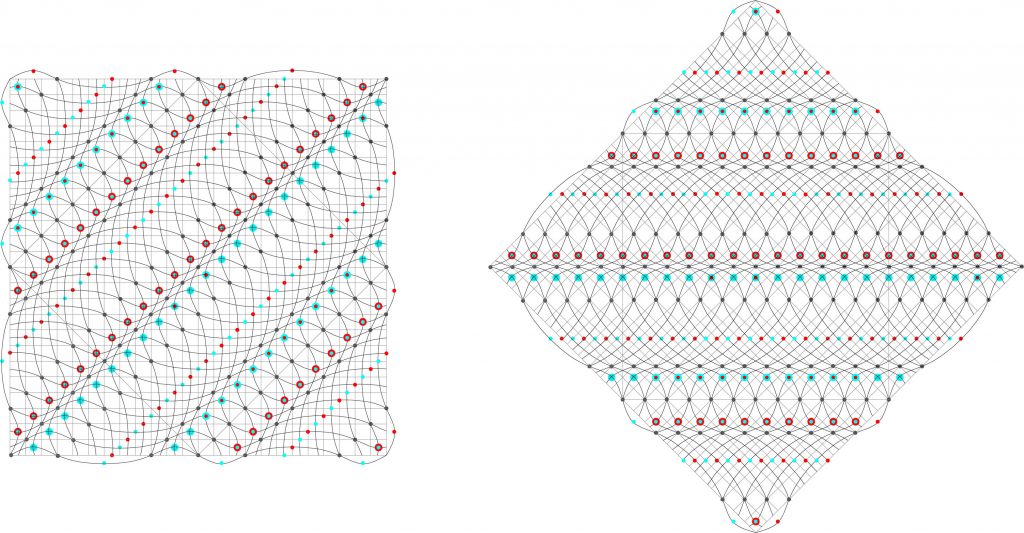
Esto es, la matriz de puntos establece un orden donde cada punto marca una posición y una condición. Por ello la membrana se ha convertido en un campo: espacio cualificado y definido geométricamente. Fig.36

Podríamos generalizar diciendo:

Si un proyecto es una de las posibles formalizaciones de una idea en el tiempo. Si todas las dimensiones de este proyecto corresponden a un sistema armónico o proporcional de medidas, la geometría del proyecto como estructura profunda de la arquitectura, está necesariamente vinculada a la música y no estaríamos lejos de comprender la afirmación de Goethe₂₇ cuando decía que la Arquitectura es Música congelada en el Tiempo.

Pero no solo eso, llegados a este punto podemos revisar todo lo planteado. Es decir, y si damos la vuelta a todo el proceso?. Y si las membranas o matrices a las que hemos analizado como un principio o semilla, son realmente los campos en los que los polígonos son sólo manifestaciones?. O dicho de otra manera, ¿no son acaso estas membranas patrones y modelos organizativos que llevan intrínsecamente unidos los conceptos de proporción y armonía?.

Esto es, en nuestro camino paso a paso, hemos vinculado las proporciones musicales con la geometría, los acordes con los triángulos y este vínculo ha introducido en la geometría, el aspecto temporal de cualquier objeto. Aspecto que ha afectado a la visión de la geometría euclídea, donde el objeto (polígono) se ha convertido en una retícula de curvas de frecuencia y que como tal, puede someterse a procesos de transformación. Pero no sólo eso, en el propio concepto de onda está contenida su manifestación como propagación de energía y de nuevo, la visión ha cambiado.

Hemos pasado del plano al espacio: al mundo de las membranas que se extienden y propagan. En definitiva, a campos que intrínsecamente están estructurados con las propias leyes de la proporción y la armonía…. O dicho de otra manera: la proporción y la armonía han devenido en patrones dinámicos o modelos energéticos de organización del espacio.

Desaparecen los triángulos, los polígonos (objetos o partículas como manifestaciones) y permanecen sólo los campos… Campos como entidades con vida propia en los que la triada de origen: Número, Segmento y Sonido₂₈ se ha mirado en el espejo y ha reflejado una nueva triada: Energía, Forma y Geometría que definen y califican a las membranas. Membranas que se han convertido en campos energéticos con leyes y estructura armónica: patrones armónicos y dinámicos de organización del espacio.

Maria Luisa López Sardá
Dr. Arquitecto

Notas a pié de página de las cuatro partes:

1.- López Sardá, Mª Luisa (2012) Acordes Arquitectónicos: Otra geometría de la proporción y la armonía en la arquitectura. Madrid. Editorial Fisuras de la cultura contemporánea

2.- Platón. Diálogos: Timeo. (1979). México. Ediciones PorrúaS.A.

3.- Vitrubio. Los diez libros de Arquitectura: LibroI.Cap.II .(1955).Madrid. Ediciones Iberia

4.- Kaku, M. Universos paralelos. (2008) Madrid. Editorial Atalanta.

5.- Greene, Brian. El Universo Elegante. (2007). Editorial Crítica SL. Drakontos Bolsillo

6.- Kaku, M. Universos Paralelos. Idem anterior

7.- Capra, F. El punto crucial. (1992). Editorial Pax. México.

8.- Es interesante aclarar la distinción que hace R. Penrose sobre el cálculo infinitesimal. Dice que este está construido sobre dos ingredientes básicos: la diferenciación y la integración. El cálculo diferencial está relacionado con velocidades y aceleraciones, con pendientes y curvatura de curvas y superficies y cosas similares. Son tasa de cambio de las cosas. El cálculo integral está relacionado con áreas y volúmenes, con centros de gravedad y con muchas otras cosas de esa misma naturaleza. Penrose,R. El Camino a la Realidad. (2007) Random House Mondadori S.A.

9.- Matemáticamente, a los distintos modos de vibración de una cuerda, se les llama los armónicos superiores de una única cantidad compleja eix= cos x+i sen x, para un período L=2π, de manera que e i2πxL, sen(2πnx/L), cos(2πnx/L), donde n= 2,3,4… Penrose,R. El Camino a la Realidad. Idem anterior.

10.- Este sistema de análisis consiste en el estudio de formas de ondas complejas mediante su descomposición, o superposición de un número suficientemente grande, de ondas básicas o armónicos.

11.- Se define la elongación como el valor de la perturbación en un determinado punto o instante siendo su valor máximo la Amplitud. Cuando la elongación varía sinusoidalmente con el tiempo según la ley y=A.senω.t donde y=elongación, A=amplitud, t=tiempo, ω=pulsación, recibe el nombre de onda armónica. La Enciclopedia El Pais. Tomo nº 15. (2003) Salvat Editores S.A.

12.-     3/2=1/1+1/2

13.-     4/3=1/1+1/3

14.-     5/3=1/1+2/3

15.- Platón. Diálogo Timeo. Idem anterior.

16.- “Por esto debemos escoger el más bello entre esta multitud de triángulos si queremos empezar convenientemente”. Platón. Diálogo Timeo. Idem anterior

17.- El isósceles de 36º/36º/108º, como gnomon del segundo: si tomamos la base como valor unidad, sus otros dos catetos toman el valor de 1/ phi . El segundo isósceles de 36º/72º/72º: si tomamos la base como valor unidad, sus otros dos catetos toman el valor de  phi.

18.- En este triángulo isósceles si tomamos la base como valor unidad, su altura es (1+√2)=

19.- En el isósceles de 30/75º/75º si tomamos la base como valor unidad, su altura es (2+√3).

El escaleno de 45º/60º/75º está formado por la escuadra y el cartabón.

20.- Platón. Diálogo Timeo. Idem anterior

21.- Las notas sostenidas suelen ser más próximas a la siguiente nota mientras que los bemoles suelen ser más próximos a la nota anterior; por ellos podemos considerar que el valor 13/8 funciona como un Sol#.

22.- El mismo criterio anterior para considerar el valor 13/12 como un Do#; así, la relación 13/12 contenida entre 1/1 y 9/8 es más próxima a 9/8.

23.- De nuevo, el mismo criterio; podemos considerar el valor 7/6 como un Mi b.

24.- Schönberg, A. El Estilo y la Idea. Idea Books.

25.- Roger Penrose. El Camino a la Realidad .Idem anterior

26.- Una imagen digital es una representación de una imagen (que tiene dos dimensiones) como un conjunto finito de elementos pictóricos o píxeles a los que se les asigna, a cada uno, un valor determinado. En términos de percepción, el paso de una entidad continua a una discreta se describe fundamentalmente como un cambio de un ente indivisible y consistente a un objeto completamente segmentado en la que incluso, sus elementos más simples (píxel) pueden percibirse individual y separadamente. Real Jurado, P.Digitalización de imágenes y topología. Dpto. Matemática Aplicada. E.T.I.I. Universidad de Sevilla

27.- Honour, H. Romanticism. (1979). Harper& Row.

28.- “Para la visión antigua, el número, el segmento y el sonido se correspondían y eran símbolo de una trascendente unidad”. Borchers, J. La medición como sustrato del fenómeno arquitectural. (Marzo-Abril 1970).   Revista Hogar y Arquitectura Nº 87.