Anotaciones a otra geometría de la proporción y la armonía. Parte 3

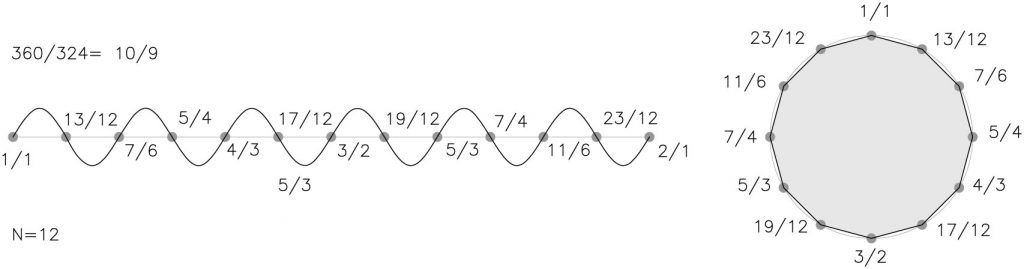
Vamos a estudiar esa “otra” geometría de la proporción y la armonía mediante el dodecágono. Este polígono por su sencillez, es un medio idóneo para entender todo el proceso, actúa como el abecedario para la construcción de las sílabas que se convierten en palabras, luego en frases y forman un lenguaje y contiene en nº suficiente de triángulos para ver la gran riqueza de soluciones y las posibilidades contenidas en la geometría de ondas de un polígono de doce lados. Fig. 20

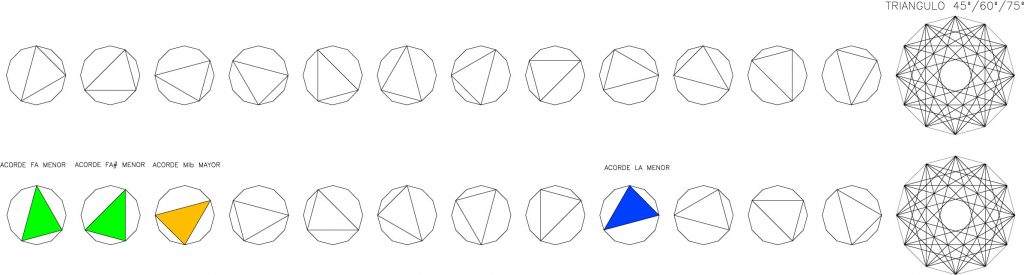
Recordemos que el dodecágono es el primer polígono que puede generarse por los tres triángulos platónicos además del isósceles de 30º y el escaleno de 45º/60/75º. Fig.21

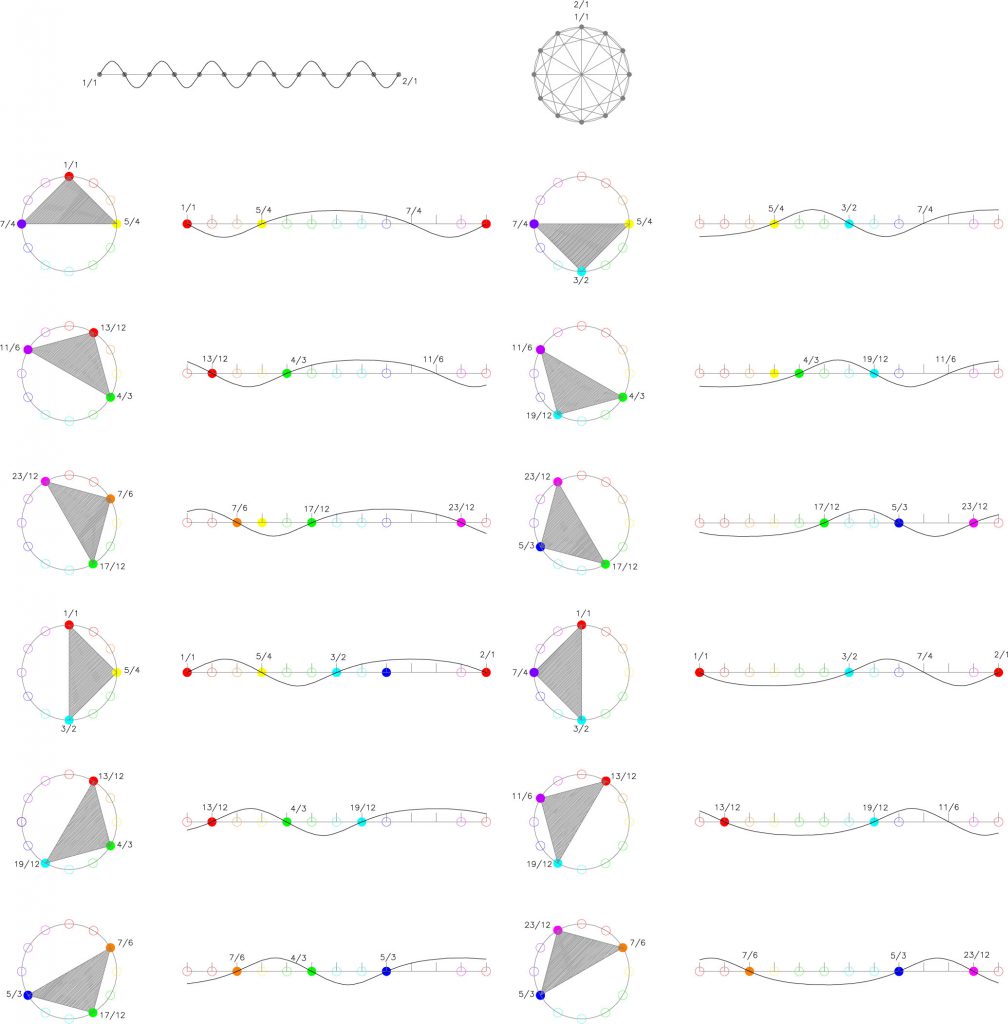
El movimiento dextrógiro de cada tipo de triángulo sobre los vértices del dodecágono produce en cada caso, una construcción geométrica única y diferente y en el proceso se hace notar las posiciones de los triángulos que pueden corresponder con acordes musicales. Fig.22, 23, 24, 25, 26 y 27.

No hay que olvidar que estas cristalizaciones no son estáticas. Han sido generadas por el movimiento de cada tipo de triángulo en el tiempo y están inscritas en la circunferencia cuya longitud es la longitud de la cuerda inicial. Si de nuevo, estiramos la cuerda pautada por los nodos o vértices de cada tipo de triángulo, podemos convertir cada posición de cada triángulo en una curva de frecuencia musical y el resultado es una única “forma de onda” de curvatura variable.

Aunque hemos mencionado las cinco diferentes construcciones geométricas que generan los triángulos constitutivos del dodecágono, todo el desarrollo que vamos a seguir exponiendo estará centrado exclusivamente en el examen de la geometría de la escuadra como ejemplo de esa “otra” geometría de la proporción y la armonía contenida en un triángulo de un polígono regular. Para el estudio se ha tomado el criterio de mantener la amplitud de origen de la cuerda y el sentido dextrógiro de giro.

Situemos el ángulo recto en la posición 1/1 y comencemos el giro sucesivo de la escuadra sobre cada vértice del dodecágono con el ritmo 3/6/3. Recogemos la totalidad de las posiciones de la escuadra y sus “formas de onda” y recordemos la dualidad onda-partícula…. Fig.27

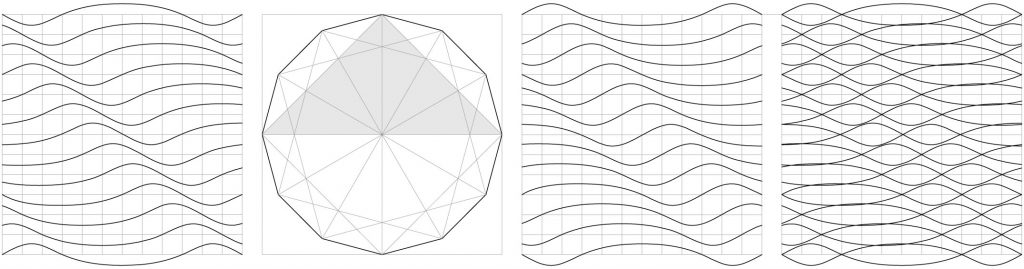
Podemos establecer una retícula de la misma longitud de la cuerda espaciada por la distancia entre los nodos e ir colocando las diferentes curvas de frecuencia de la escuadra en su orden correspondiente de generación. Estas retículas son en sí, no dependen de medida al igual que el dibujo geométrico.  Son instantáneas congeladas en el tiempo y actúan como semillas que contienen la génesis de cada construcción geométrica. Es una convención que se establece para entender como síntesis esta generación del dodecágono desde el punto de vista ondulatorio. Y por ello, también pueden ordenarse sobre el eje vertical. En ambos casos representan bien en longitud, bien en altura la forma sistemática de vibración del dodecágono según su triángulo característico, en este caso, la escuadra.

En el siguiente dibujo se ha situado a cada lado de la figura geométrica ambas oscilaciones de la cuerda (una como onda incidente y la otra como onda reflejada) y el cuarto dibujo reproduce cada posición de la escuadra como onda estacionaria. Fig.28

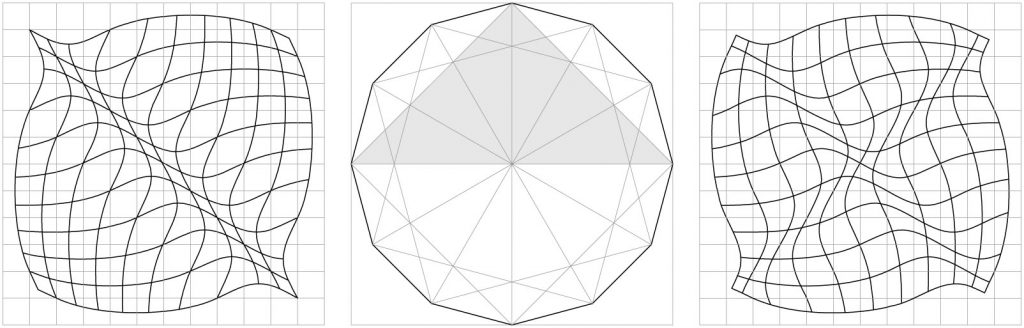
Así como podemos superponer dos figuras geométricas manteniendo sus condiciones de simetría, igual podemos hacer con las diferentes retículas obtenidas de los diferentes triángulos. Si entrecruzamos ambas retículas horizontal y vertical, empezamos a encontrar que no sólo la retícula base vibraría en una dimensión o dirección sino que la propia retícula se “arrugaría” formando superficies de valles y crestas dando origen a membranas vibrantes en el tiempo.

Se han utilizado dos criterios de superposición aunque ambos utilizan la ortogonalidad. El primer criterio, representado a la izquierda plantea un giro de 90º y su espejo. El segundo criterio, representado a la derecha supone un giro de 90º. Pero lo más importante es que la ortogonalidad de ambos criterios de superposición nos ha introducido desde el mundo del plano al mundo del espacio. Fig.29

Tal vez lo más llamativo de la figura anterior es ver la figura geométrica en el centro, rodeada por dos tipos de membrana, consecuencia de su aspecto ondulatorio y de los criterios de superposición. Esto significa que una de las características esenciales de la geometría, la dimensión o la extensión, es decir, la longitud, anchura y altura, ha sido sustituida por la amplitud y la longitud de onda, lo que implica la introducción del tiempo como generador. Esto es: frecuencia, pulsación, velocidad y sobre todo, energía porque recordemos: una onda es una forma de propagación acompañada de una transmisión de energía….

Y estas semillas-membranas tienen capacidad de extenderse y propagarse… Esta capacidad de extensión de las membranas con leyes de formación y características propias,

– ¿no es acaso el concepto de campo de la mecánica cuántica?. ¿Un campo no se extiende en una zona mucho más amplia que la que ocupa la partícula?.

– ¿No supone esto un cambio en la percepción del propio objeto, el polígono, hacia un proceso de patrones y modelos organizativos?.

– Así como en física se considera que una partícula es una expresión manifiesta de un campo, ¿podríamos considerar los polígonos regulares (como objetos o partículas) como expresión de patrones o membranas ondulatorias?

– ¿Acaso la agudeza de los ángulos de un triángulo en su conversión a curvas de frecuencia, no indica mayor frecuencia o velocidad de ondulación y siguiendo a Einstein, en definitiva, en mayor gravedad con lo que supone de mayor arrugamiento del continuo espacio tiempo y por tanto de forma o límite más característico?

Esta foto está tomada en una piscina. El volumen del agua casi  quieto permite ver el fondo de esa manera. Un ejemplo que permite mostrar que lo que estamos describiendo no está tan lejano de la vida cotidiana…. Fig. 30

(continua en Parte 4)