(Los poliedros regulares y la definición del espacio)
En una de las últimas visitas, allá por 2018, con José Luis Bozal y José Carlos Velasco al monasterio de Poblet (Tarragona) a fin de “mirar con otros ojos” la investigación realizada hasta ese momento además de las últimas comprobaciones sobre determinadas medidas de la iglesia y del monasterio (1), sucedió que recorriendo lentamente de nuevo la iglesia y en especial, el ábside, la atención se fijó en unas pequeñas esculturas situadas en las basas o plintos de las columnas del ábside y justo, a la izquierda en la primera columna mirando hacia el altar, aparece una esfera y un rombicuboctaedro. F1 y F2

En el libro mencionado se dedica una parte de la investigación a este hecho. Han pasado los años y he vuelto a encontrar al rombicuboctaedro en otras circunstancias y también con otro conocimiento.

Sucede que pensamos y vivimos el espacio como la nada vacía que permite cualquier configuración …Y ya entonces, en los años 40 del siglo pasado, Richard Buckminster Fuller nos advertía:
“El espacio tiene forma, características específicas que no sólo podemos enumerar y comprender sino también empezar a sentir sus cualidades envolventes, esa sensación de espacio estructurado que impregna toda experiencia.”(2)
También Arthur Loeb apuntaba:
“El espacio no es un vacio pasivo sino que tiene propiedades que imponen poderosas restricciones a cualquier estructura que lo habite…” y añadía:
“… y estas restricciones son independientes de las fuerzas específicas, de los materiales de construcción, del tamaño, etc, sólo dependen de “la propia naturaleza geométrica del espacio””. (3)
Ampliamente conocidos desde la antigüedad, Fuller se dio cuenta de que los poliedros regulares (las eternas formas de geometría llamados sólidos platónicos), no eran “sólidos o formas cerradas inmóviles”; en realidad eran un “modelo de relaciones” entre aristas, vértices y caras (4). Esa nueva forma de ver y comprender le condujo a los orígenes de ellos; percibió que no éramos totalmente conscientes de lo que estos poliedros significaban y de sus implicaciones sobre el espacio mismo.
Y así comenzó afirmando (5):
– no existe el punto adimensional, existe un evento de energía.
– no existe la línea, son trayectorias onduladas o fragmentadas.
– no existe el plano continuo, existe una malla de eventos energéticos inter-relacionados por vectores diminutos, porque existen fuerzas que tiran o empujan y que pueden modelarse como “vectores” con longitud y ángulo.
– no existen los sólidos, la materia consiste exclusivamente en energía. Las cosas son en realidad eventos, disposiciones transitorias de movimiento atómico vibrando frenéticamente. La energía tiene forma. Se transforma y transfigura de forma evolutiva.
Estas primeras afirmaciones son principios a los que llamó “generalizables”, fundamento de la continua investigación de Fuller a lo largo de su vida sobre el “sistema de coordenadas de la naturaleza” (6). Investigación que llamó en principio, Geometría Sinérgica.
Geometría como ciencia de los sistemas o configuraciones y estudio de sus relaciones. Sinergia como comportamiento de sistemas completos no predichos por el comportamiento de las partes tomadas por separado, porque el todo es más que la suma de las partes.
Posteriormente lo nombró Sinergética: como articulación geométrica de las relaciones energéticas cuyas matemáticas están basadas en la Topología y la Geometría vectorial (201.01). Rama de las matemáticas que estudia la estructura de la naturaleza de acuerdo a requisitos mínimos de energía. Una función de la interrelación entre fuerzas físicas y limitaciones espaciales. Investigación recogida en los libros que R.B.Fuller tituló: “Sinergetics: Explorations in the Geometry of Thinking” .(7) En la sección 200.00 de “Synergetics: Definitions”, y siguientes, Fuller plantea el alcance, características y postulados que engloba dicha definición.

Centrándonos en los poliedros, conviene recordar algunos conceptos básicos sobre esta geometría de los sólidos platónicos.
Empezamos por la propia definición de poliedro regular:
– Modelo espacial cerrado formado por caras idénticas y mismo número de ellas en cada vértice; caras idénticas formadas por polígonos regulares coincidentes en cada vértice del poliedro. F3

Recordar la definición de Euler:
– Todos los poliedros están formados por tres elementos: cruces, líneas y superficies abiertas. Esto introdujo los elementos básicos de su estructura: vértices, aristas y caras (vértice=punto=a0, arista=línea=a1 y superficies=caras=a2). A estos mismos elementos Fuller los distinguió nombrándolos como vórtices, vectores o líneas de energía y caras como red de eventos.
Recordar también la ley de Euler, que establece:
– El número de vértices más caras es igual al número de aristas más 2. Esto es: V+C=A+2. O dicho con otras palabras: la diferencia entre la suma del número de caras y vértices y el número de aristas será siempre 2. Esto es: V+C–A= 2
Por último, acercándonos a ese entendimiento de Fuller y alejándonos de esa concepción tradicional de poliedro como “sólido platónico”, recordemos su afirmación de que “el tetraedro es la unidad básica de la dinámica energética de Universo,(986.048)” o con otras sus palabras, “el aspecto más primario de la estructura geométrica del espacio (987.091b)”.
Por ello, vamos a recordar concisamente, el proceso de nacimiento de estos 5 poliedros cuyas caras son polígonos regulares. (8)
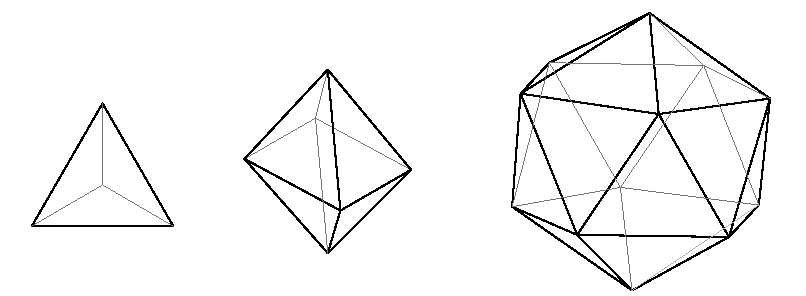
Empezamos en dos dimensiones con el mínimo polígono, el triángulo equilatero.
– Para poder formar una estructura espacial, el mínimo número de caras alrededor de un vértice serían tres (3×60º=180º). Tres aristas o tres caras equiláteras alrededor de un vértice forman una pirámide cuya base automáticamente es otro triangulo equilátero. Por ello, 4 caras iguales, 4 vértices trivalentes (con tres aristas) y 6 aristas, forman el mínimo poliedro o tetraedro, primer sólido platónico que engloba el mínimo volumen y la mayor superficie de cerramiento. F4
– Si reunimos 4 triángulos en un vértice se forma una pirámide cuya base automáticamente es un cuadrado con 4 aristas por vértice (4×60º=240º) para cerrar esa estructura espacial. Dicho cuadrado o plano de simetría da forma al poliedro de 8 caras iguales con 6 vértices tetravalentes (con cuatro aristas) y 12 aristas u octaedro. F5
– Si reunimos 5 triángulos en un mismo vértice produce una base pentagonal; son necesarias por tanto, 5 aristas por vértice (5×60º=300º) para formar una pirámide de poca altura, que las caras mantengan la forma del triángulo y puedan cerrar esa estructura espacial. Esto conduce al icosaedro: 20 caras triangulares, 12 vértices pentavalentes (con cinco aristas) y 30 aristas; tercer poliedro platónico. F6
No podemos reunir más triángulos alrededor de un vértice puesto que 6×60º = 360º define un plano. No es posible un cerramiento espacial con más de 5 triángulos equiláteros. Luego ya tenemos, según R.B.Fuller, la primera limitación espacial: No podemos tener menos de 2 y más de 5 triángulos equiláteros por vértice para crear un sistema espacial cerrado.
Seguimos con el cuadrado en dos dimensiones como cara de poliedro.
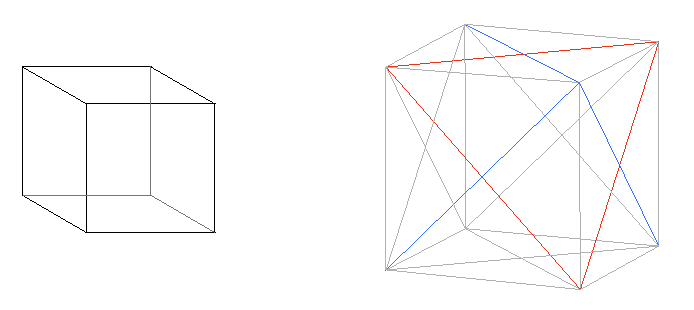
– La única disposición posible es de 3 cuadrados reunidos en un vértice o 3 aristas por vértice (3×90º= 270º) cuya composición permite formar una estructura cerrada espacial. Este es el cubo o hexaedro: poliedro de 6 caras cuadradas, 8 vértices trivalentes y 12 aristas F7. Recordemos también que dos tetraedros entrelazados con un centro de gravedad común definen también los 8 vértices del cubo. F8
Segunda limitación espacial: No podemos tener ni menos ni más de tres cuadrados para crear un sistema finito cerrado y el único sistema es el cubo.
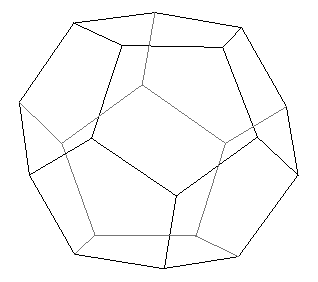
Mismo proceso con el pentágono: Tres caras alrededor de un vértice o 3 aristas por vértice (3×108º=324º) forman una pirámide de poca altura cuya composición permite formar una estructura cerrada espacial: el dodecaedro compuesto de 12 caras pentagonales, 20 vértices trivalentes y 30 aristas. No hay más posibilidades de reunir pentágonos alrededor de un vértice (cuatro superarían los 360º del plano) y con ello, tenemos la tercera limitación espacial. F9
Llegamos al final del proceso. Un sólo hexágono alrededor de un vértice ya no permite un sistema espacial pues sus 360º forman un plano. Y así sucesivamente con los siguientes polígonos regulares.
El espacio ha impuesto sus reglas y sólo cinco sistemas o poliedros han sido configurados con capacidad de cerrar el espacio con las condiciones de las que hemos partido. Por ello, sólo son cinco los poliedros regulares. F10
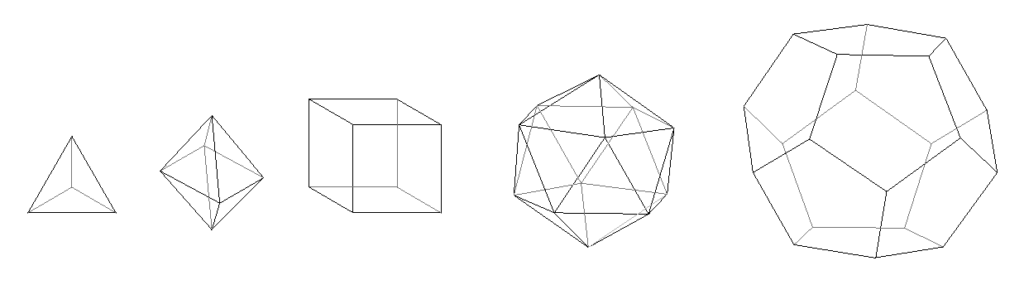
Aplicando la ley de Euler encontramos que en cada caso:
– Tetraedro. 4V+4C = 6A+2
– Octaedro. 6V+8C = 12A+2
– Cubo 8V+6C = 12A+2
– Icosaedro 12V+ 20C = 30A+2
– Dodecaedro 20V+ 12C = 30A+2
Si nos fijamos en la tabla anterior, veremos que, a excepción del tetraedro, los cuatro siguientes poliedros intercambian dos a dos, el número de caras y de vértices y mantienen el mismo número de aristas.
– Si el octaedro tiene 6 vértices y 8 caras, el cubo tiene 6 caras y 8 vértices.
– Si el icosaedro tiene 12 vértices y 20 caras, el dodecaedro tiene 12 caras y 20 vértices.
El octaedro y el cubo, el icosaedro y el dodecaedro son considerados poliedros duales. Poliedros con una dualidad: 1) numérica como coincidencia precisa de vértices con caras, pero también 2) geométrica puesto que si unimos los puntos medios de las caras de un cubo obtenemos un octaedro y viceversa. F11
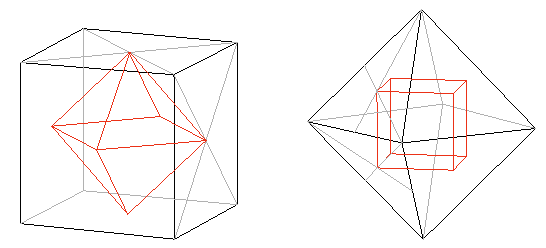
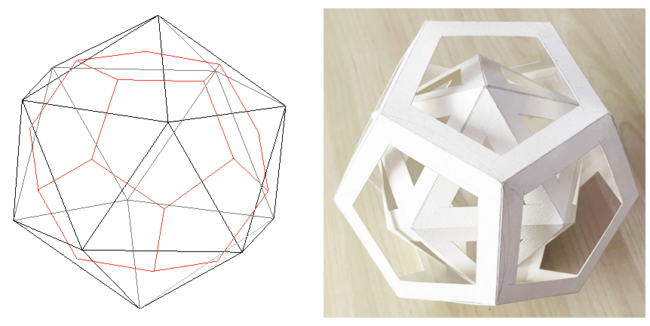
Igual sucede con el icosaedro y el dodecaedro, los centros de las caras del dodecaedro son los vértices del icosaedro. F12 y F13
Y en esta historia, sólo el primero, el tetraedro, es el dual de sí mismo. Si unimos los centros de las caras triangulares, obtenemos otro tetraedro. F14
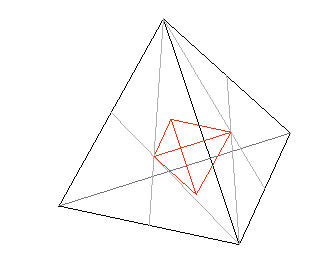
Es decir, esas dualidades son relaciones estrechas, dos a dos, entre cuatro de los propios poliedros sobre las que volveremos.

Partiendo de estos cinco poliedros, hay cinco operaciones geométricas conocidas también desde antiguo que han generado una gran variedad de nuevos poliedros llamados semirregulares. Nos centraremos en las dos más conocidas.
La primera se conoce como truncamiento. Consiste en cortar los vértices de cada poliedro formando un plano hasta constituir una nueva figura o sistema espacial cerrado . Esto es, sustituir un vértice (a0) por una superficie o plano (a2). El corte de un vértice de tres aristas o tres caras producirá un triángulo, si el vértice es de cuatro aristas o cuatro caras, el corte resultante será un cuadrado, etc. Esto es, el número de aristas en cada vértice generará un nuevo polígono regular dependiendo de la amplitud del corte en la arista, producirá otros nuevos poliedros; pero el límite está en el punto medio de dichas aristas donde se tocan o coinciden los planos de truncamiento de cada vértice.
La segunda operación se conoce como estelación. Es el procedimiento dual o contrario al anterior y el origen de los poliedros estrellados. En vez de cortar o quitar, consiste en añadir o sumar una pirámide a cada cara del poliedro. En este caso, el límite de la estelación se produce cuando la altura de las pirámides agregadas a cada cara es tal que sus caras se vuelven coplanares con las del poliedro a estelar.
Estas dos operaciones geométricas han dado origen a los llamados poliedros semirregulares. Entre ellos, hay un grupo de 13 llamados arquimedianos, que mantienen sus caras regulares (pero no todas iguales), y vértices iguales y por ello, el mismo número de aristas por vértice.(9) F15
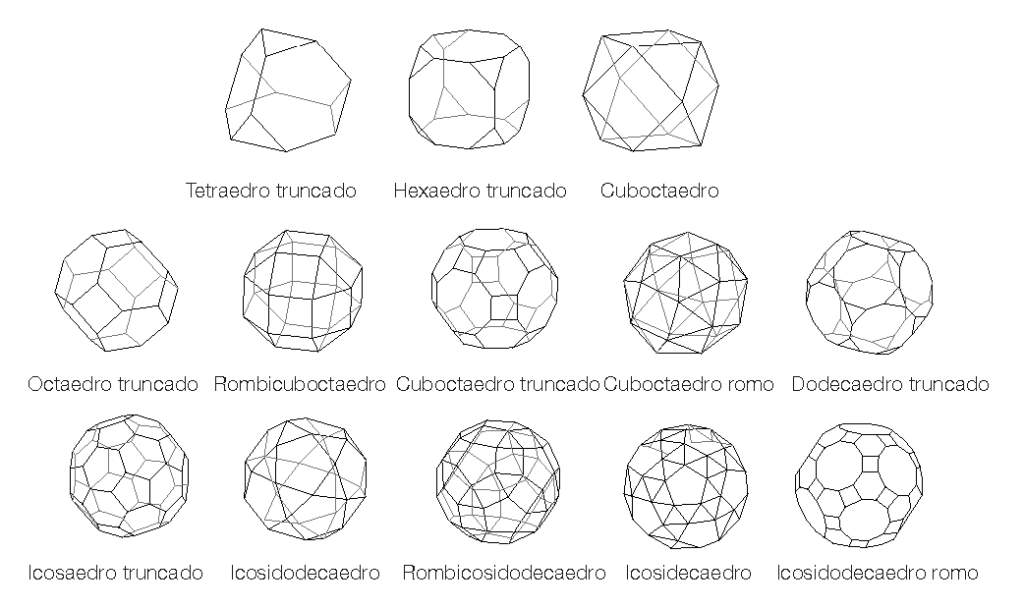
Siete de ellos se obtienen por truncamiento de los poliedros regulares. Y en este grupo encontramos dos sobre los que nos centraremos: el cuboctaedro y el rombicuboctaedro. También mencionaremos otro poliedro semirregular, el dodecaedro rómbico clasificado como sólido de Catalán compuesto de 12 caras rómbicas. Poliedro al que más adelante dedicaremos un tiempo. F16, F17 y F18


El cuboctaedro surge del truncamiento de los vértices de los poliedros, cubo y octaedro, hasta la mitad de sus aristas (por lo que éstas desaparecen). Es un poliedro semirregular compuesto de 12 vértices, 24 aristas y 14 caras (= 6 cuadradas y 8 triangulares). O dicho de otra manera, formado por 8 tetraedros y 6 medioctaedros. Si el cubo tiene 6 caras cuadradas y el octaedro ocho caras triangulares, el cuboctaedro tiene 6 caras cuadradas y 8 caras triangulares. F19 y F20
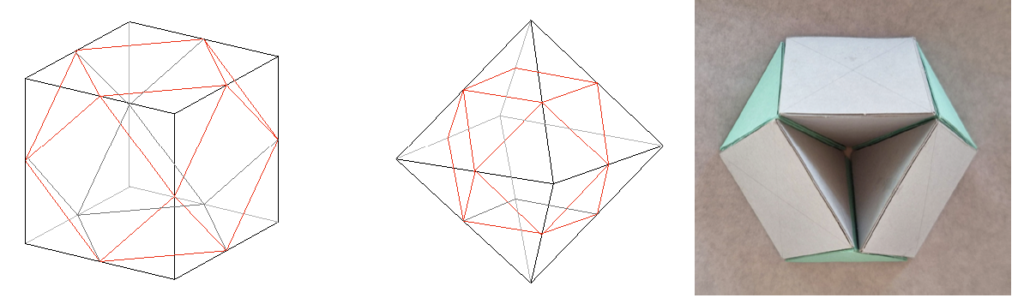
Esta figura tiene una serie de características que la convierten en un sistema espacial “especial”: F21
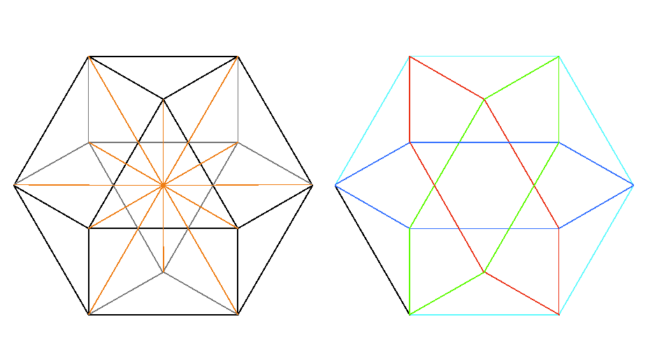
– Las 24 aristas y los 12 radios que salen de su centro a cada vértice son iguales.
– Contiene 4 planos de simetría: cuatro hexágonos simétricamente organizados en los cuatro planos girados 60º.
– Mismo número de caras por vértice. (4= 2 equiláteros + 2 cuadrados)
– Todos los vértices son puntos de una esfera.
– Cumple la ley de Euler : 12V+14C= 24A+2
El cubooctaedro, rebautizado por B. Fulller como “equilibrio vectorial” juega un papel esencial en su Sinergética o Geometría Sinérgica, es la piedra angular. Fuller lo definió:
“Vector Equilibrium: is the zero starting point for happenings or nohappenings, it is the empty theater and empty circus and empty Universe ready to accommodate any act and any audience. Synergetics (2nd.Ed) at Sec.503.03; 11Dec.1975 (10)»
Al plantear Fuller que los sólidos platónicos eran representaciones de diagramas de vectores en los que cada arista, como vector, era una línea de longitud especifica y determinada orientación angular y por ello, una posible representación de fuerzas (puesto que la magnitud viene dada por la longitud del vector-arista y su dirección por la orientación angular), Fuller los incorporó como diagramas geométricos que definen una forma (una forma es exclusivamente angular y por tanto, independiente del tiempo) y un tamaño o dimensión (dependiendo del tiempo).(11)
Esa representación del cuboctaedro como vectores de energía donde todos son iguales en fuerza y donde cualquier diferencia de presión, carga, fuerza, spin, etc lleva al campo fuera del equilibrio, tiene consecuencias más profundas puesto que, justo en ese instante es cuando se observan “diferencias”, nacen las relaciones, la “ nada” se convierte en “algo”…surge la dualidad y una entidad se manifiesta. En ese instante, más importantes que las caras son los vértices o vórtices que definen la forma, por ser los puntos de intersección de los vectores de energía. F22.
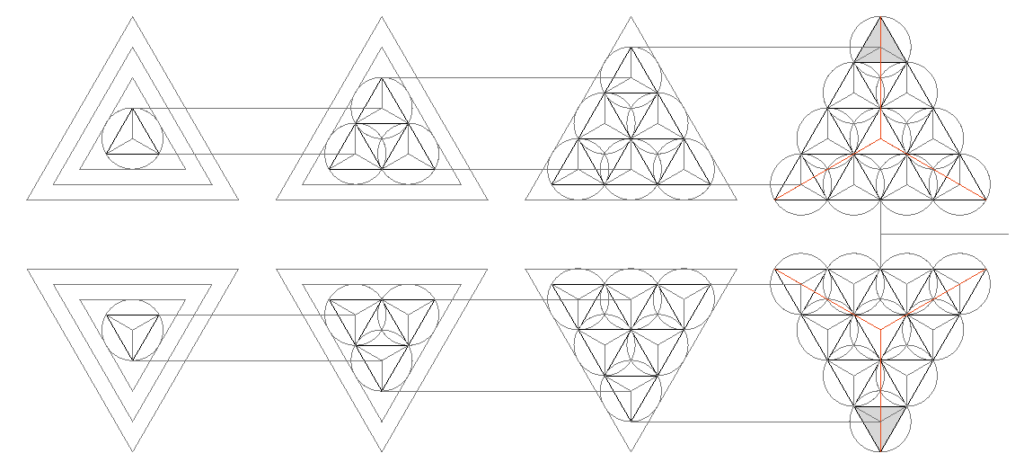
Como ya hemos mencionado, Fuller definía al tetraedro como el aspecto más primario de la estructura geométrica del espacio y el cuboctaedro representaba la matriz geométrica de energía más primaria del cosmos puesto que todos los vectores que irradian de su centro tienen la misma longitud y por tanto, están en equilibrio así, las fluctuaciones se hacen invisibles y por eso lo llamó la Fase Cero de todas las dinámicas de energía. Al ser una geometría de vectores y ángulos iguales de 60º, era posible extenderla indefinidamente hacia fuera desde su punto central, generando lo que llamó Matriz Vectorial Isotrópica. F23
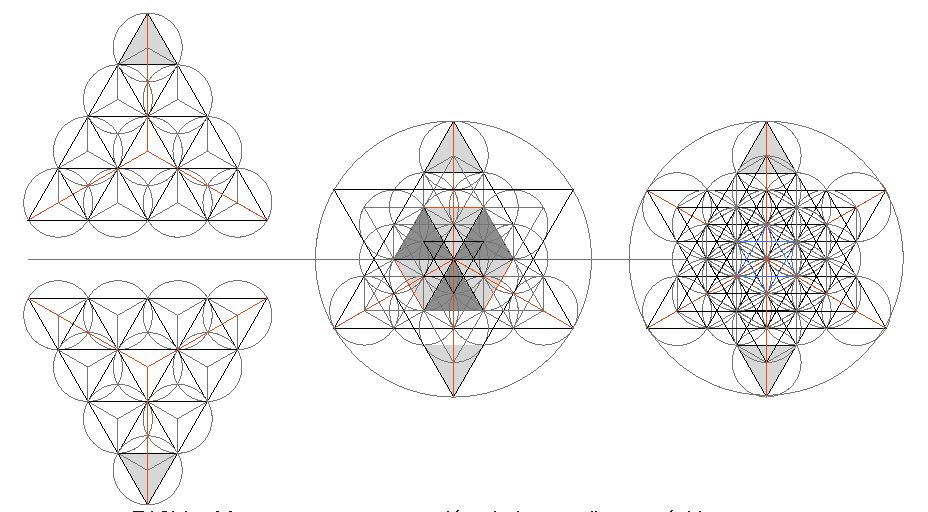
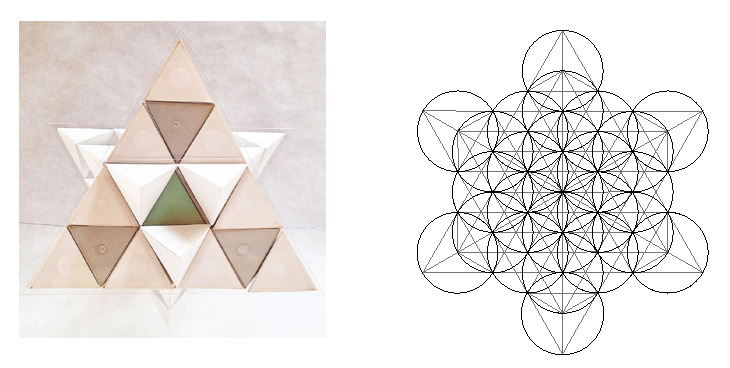
Matriz en cuanto patrón, Vectorial en cuanto mismas líneas de energía e Isotrópica porque en todas las direcciones sucede lo mismo; esto es, en todas direcciones las mismas condiciones de energía. Una disposición sencilla de geometrías alternas de tetraedros y octaedros. Algo así como el “esqueleto estructural energético”.
El equilibrio vectorial o cuboctaedro al tener sus caras cuadradas, intrínsecamente inestables, contienen la capacidad de movimiento, la fase cero (zero starting point) del cual emergen todas las formas… Este movimiento intrínseco al poliedro, va unido a su pulsación, como expansión o contracción y, de nuevo, las investigaciones de Fuller definen el proceso.
Si aplicamos al cuboctaedro una fuerza de contracción a dos de los vértices de las caras cuadradas, la diagonal que los une va disminuyendo su distancia; cuando la medida de ella iguala la medida de la arista, el cuadrado se ha convertido en un rombo formado por dos triángulos equiláteros; esto aplicado en todas las caras cuadradas hace que el sistema se convierta en un icosaedro. Fuller lo llamaba fase icosaédrica. (13)
Según Robert Gray (14), al ser el dodecaedro dual del icosaedro, éste poliedro también está implicado energéticamente y continuando el movimiento de contracción de las caras cuadradas del cuboctaedro, se llega a una fase dodecaédrica hasta que la distancia entre diagonales desaparece y queda la forma final octoédrica.
Esto es, el cuboctaedro, formado por tetraedros y medios octaedros, es afectado por una dinámica de “jitterbug» (bailarín de jazz) como lo llamó Fuller (15), que manifiesta energéticamente las estructuras platónicas de los cinco poliedros regulares. Por ello, Fuller especifica que estas condiciones de partida del cuboctaedro le permiten representar un diagrama geométrico de equilibrio espacial. F24
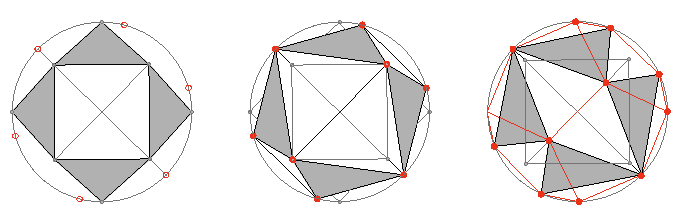
Hemos aplicado el truncamiento al cubo y al octaedro, obteniendo en ambos casos el cuboctaedro.
Si aplicamos la estelación a ambos poliedros, el resultado es ese poliedro de Catalán ya mencionado, en F18, y conocido como rombododecaedro o dodecaedro rómbico compuesto de 12 caras rómbicas.
Si lo hacemos en el cubo, la estelación permite añadir 6 pirámides de base cuadrada a las caras formando rombos en donde las aristas del cubo corresponden a las diagonales cortas de las 12 caras. F25 y F26.
Si la estelación la aplicamos al octaedro, se añaden 8 pirámides de base triangular y sus aristas se convierten en las diagonales largas de las caras rómbicas. F27
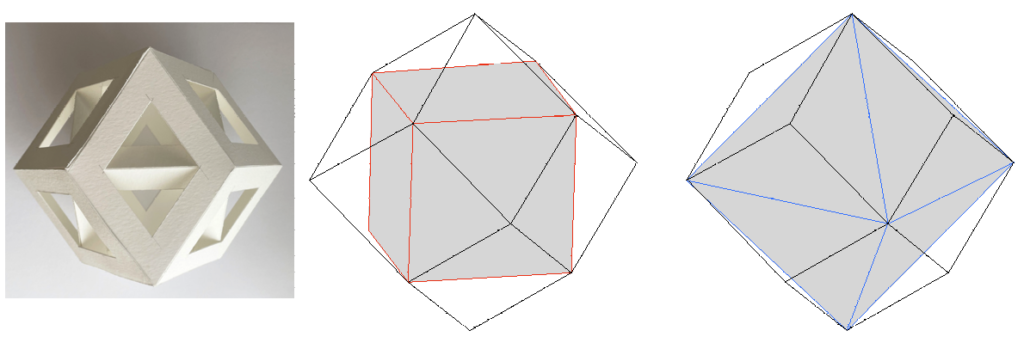
Si unimos los puntos medios de las caras del dodecaedro rómbico desaparecen 6 pirámides cuadradas y 8 triangulares en sus 14 vértices, y obtenemos el cuboctaedro. F28
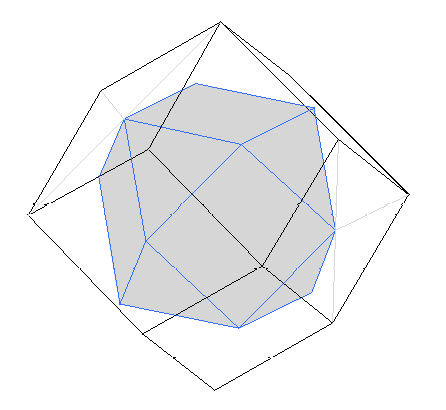
Aplicando la ley de Euler a estos dos nuevos poliedros:
– Cuboctaedro 12V + 14C= 24A + 2
– Dodecaedro rómbico 14V + 12C= 24A + 2
Resultan poliedros duales. Esto es:
– El truncamiento del cubo y del octaedro conforma un cuboctaedro.
– La estelación de los mismos poliedros conforma el dodecaedro rómbico.
– Y estos dos nuevos poliedros son duales al igual que ambas operaciones geométricas.
Esto recuerda la afirmación de Fuller de que: ”La unidad es plural […] y como mínimo dos” (16)

Llegados a este punto, enumeremos las relaciones de pareja que han ido saliendo:
– Cubo y octaedro: poliedros duales.
– Icosaedro y dodecaedro: poliedros duales.
– Tetraedro: dual de sí mismo.
– Las operaciones geométricas de truncamiento y teselación: operaciones duales.
– El truncamiento del cubo y del octaedro da origen al cuboctaedro.
– La estelación del cubo y del octaedro da origen al dodecaedro rómbico.
– El cuboctaedro y el dodecaedro rómbico son igualmente poliedros duales.
pero también las nuevas relaciones que surgen entre ellos:
– Si partimos de un tetraedro al que aplicamos el truncamiento en todas sus vértices mediante bisección de sus aristas, obtenemos en su interior un octaedro.
– Si a ese octaedro, truncamos sus vértices biseccionando sus aristas, obtenemos un cuboctaedro
– y por, último, si a este cuboctaedro truncamos y biseccionamos de nuevo, sus aristas, el poliedro obtenido es un rombicuboctaedro… F29
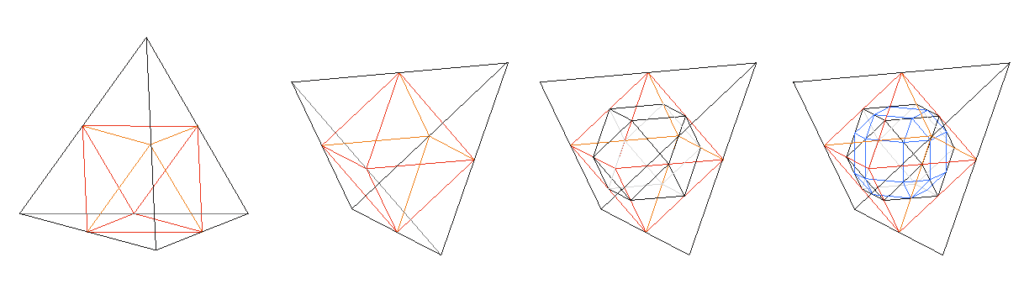
pero después de nombrar al rombicuboctaedro, Fuller se detiene en su exposición. Este proceso es citado por Amy Edmonson en el libro antes mencionado y volveremos sobre ello.
Pero no olvidemos que estamos describiendo poliedros en el Espacio-Tiempo que habitamos, descrito por la Física desde principios del siglo XX. Recordemos esa descripción de la partícula elemental como “un patrón dinámico con un aspecto espacial como objeto con una cierta masa y un aspecto temporal como proceso que encierra una energía”. (17) Hablamos del espacio y tiempo, de masa, forma y energía…

Como ya antes hemos indicado al comienzo de este escrito, dedicamos un apartado del libro, a este poliedro esculpido en una base de las columnas del ábside de Poblet.
“En el conocido retrato de Fray Luca Pacioli en el que se le representa explicando uno de los teoremas de Euclides y acompañado de un joven de aspecto noble, probablemente su protector Guidobaldo, duque de Urbino, realizado en 1495 y atribuido a Jacobo de Barbari, aparecen dos poliedros, un dodecaedro sólido apoyado sobre una caja en la mesa y un gran rombicuboctaedro transparente que parece estar lleno de líquido y colgado del techo. Este cuadro forma parte del libro de “De Divine Proportione” de Luca Pacioli. […] En el capítulo LIII de la primera parte del libro explica mediante las láminas XXXV, XXXVI, XXXVII y XXXVIII este poliedro y sus variantes como poliedros estrellados”. F30 y F31

F31. Detalle del rombicuboctaedro.
Entonces nos preguntábamos: “¿por qué el pintor seleccionaba un poliedro platónico y uno arquimediano de los 60 poliedros que Leonardo dibujó para el mencionado libro?. Podíamos entender el dodecaedro puesto que Platón lo consideraba el quinto elemento, la quintaesencia, la sustancia del cosmos pero y ¿el rombicuboctaedro? “
¿Cual sería su importancia que a principios del siglo XVI, A. Durero, en el libro IV “De la Medida” lo presenta en su desarrollo plano?”

Volvamos al siglo XV. En el libro “La Divina Proporción” (18) en el capítulo XLIX: «Del hexaedro plano sólido o hueco, absciso sólido o hueco, elevado plano y elevado absciso», Luca Pacioli le describe, “…formado por 24 aristas que originan 48 ángulos superficiales, 24 de ellos rectos y los demás agudos compuesto de 12 ángulos sólidos y conteniendo 14 superficies, 6 cuadradas y 8 triangulares…”. En las Láminas IX y X están representados bajo el título de «Exahedron Abscisus Solidus y vacuus». Y acaba la descripción : “Y este cuerpo se origina del cubo mediante el corte uniforme en la mitad de sus lados…” Nada más y nada menos que nuestro cuboctaedro. F32
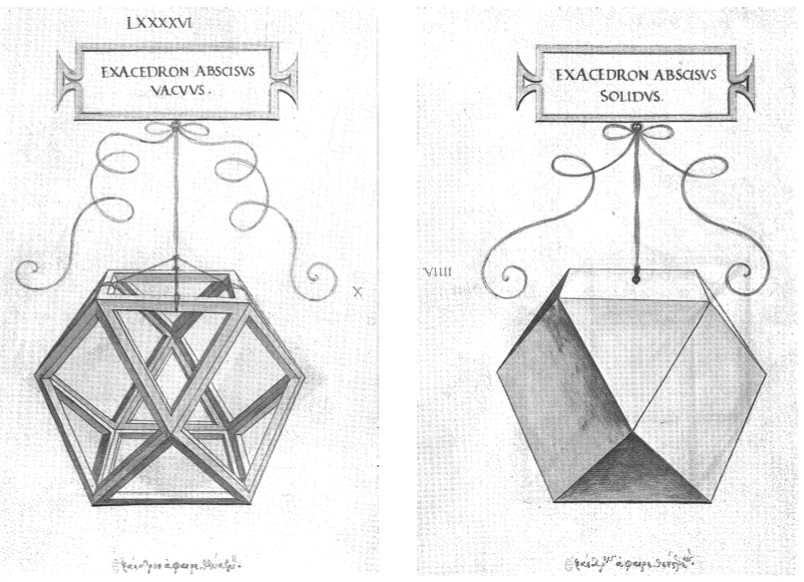
En el capítulo LIII: “Del cuerpo de 26 bases sólido o hueco y elevado sólido o hueco y su origen”, describe: “Otro cuerpo, excelso Duque, muy distinto de los nombrados es el que se llama cuerpo de veintiséis bases, de hermosísimo principio y origen derivado. De sus 26 bases, 18 son cuadradas, equiláteras y rectángulas, y 8 triangulares, igualmente equiláteras y equiángulas. Tiene 48 lados o líneas y 96 ángulos superficiales, 72 son rectos – los de sus 18 bases cuadradas – y 24 agudos – los de sus 8 triángulos equilátero”.
Finaliza la descripción diciendo (19): “el origen de este cuerpo es el hexaedro uniformemente cortado en todas sus partes […] y su conocimiento resulta utilísimo por muchas consideraciones para quien bien lo sepa aplicar, sobre todo en arquitectura”. En las láminas XXXV y XXXVI están representados bajo los títulos «Vigintisex Basium Planus Solidus» y «Vigintisex Basium Planus Vacuus». F33

Pero en ambas versiones del libro de la Divina Proporción, Luca Pacioli no menciona los duales de ambos que ya hemos descrito: el dodecaedro rómbico, dual del cuboctaedro, y el icositetraedro deltoidal, dual del rombicuboctaedro, aunque sí plantea la estelación del rombicuboctaedro en las láminas XXXVII y XXXVIII con los títulos «Vigintisex basium abscisum elevatum solidum y vacuum.» F34

Ed. Losada.

Vayamos más atrás en el tiempo. Otto Von Simson escribe en el libro “La Catedral Gótica”(20):
“Durante el segundo cuarto del siglo XII, dos vigorosos movimientos intelectuales captaron en Francia la filosofía agustiniana de la belleza. El primero tenía su centro en el grupo de eminentes platónicos que se reunían en la escuela de la catedral de Chartres; el segundo, movimiento de carácter antiespeculativo y ascético, procedía de los grandes monasterios de Citeaux y de Claraval y estaba personificado por San Bernardo […] de hecho, el arte gótico no habría existido sin la cosmología platónica que se cultivó en Chartres y sin la espiritualidad de Claraval”.
Y ambos tenía en común la herencia de San Agustín. “La autoridad de San Agustín conformó la Edad Media. El fragmento del libro de la Sabiduría de Salomón que dice “has ordenado todas las cosas en medida, número y peso” y la interpretación que le diera San Agustín, se convirtieron en la clave de la visión medieval del mundo”.
Para San Agustín: “Las funciones que asigna a la aritmética, geometría y música son fuente de la creación artística ya que la estética de San Agustín (y la de Boecio) sólo admite las razones “perfectas” de la mística pitagórica”.
Y más adelante continua: “San Agustín al igual que su discípulo Boecio que era para la Escuela de Chartes y para la Edad Media en general, la mayor autoridad en matemática, enseñaba también a hacer visibles en términos geométricos, las consonancias perfectas”.
El libro ya mencionado sobre la traza en el monasterio de Poblet, desarrolla en la Parte 2.2: De la Traza, el análisis de las trazas de la Iglesia, del Claustro, de la Sala Capitular y del Templete del Lavabo y los pasos geométricos y numéricos que conforman esas zonas del monasterio. Y en la Parte 2.3: Número, Proporción y Medida, se especifican los Números, Escuadras, Polígonos, Proporciones y Consonancias confirmadas en las trazas. (21) F35
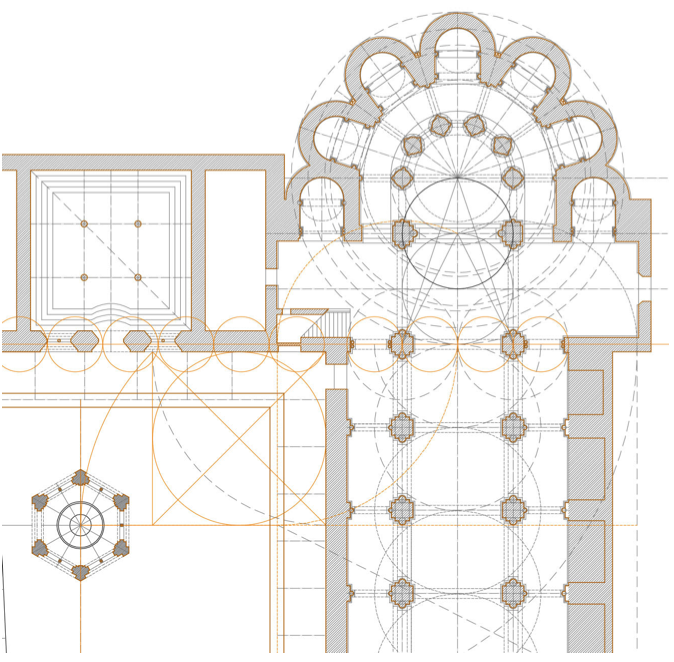

Vamos más atrás en esta línea de tiempo: Platón y su diálogo “Timeo”.
En el artículo Proporción 1: Las Medias Proporcionales (22) sobre la Lambda de Platón, generación numérica cuyo origen era la Tetractys Pitagórica, comentabámos ese vacío existente en el centro de las líneas inclinadas marcadas por las sucesivas potencias de 2 y 3; sugeríamos que podían ser rellenadas por los números 6, 12 y 18.
Se puede observar que en la F36, el 6 ocupa el centro vacio de la Lambda. Sabemos que el número de aristas de los poliedros es siempre múltiplo de ¡¡6!! (23) y podemos reconocer que el patrón geométrico que surge en la tercera figura reproduce la forma hexagonal en planta del cuboctaedro. F36.

Si recordamos los números básicos de los tres primeros poliedros:
– tetraedro 4C+4V= 6A+2, los números 4/4/6 pertenecen, en la Lambda, a la segunda potencia, y las tres relaciones entre ellos marca las consonancias 1/1 o Unísono y dos veces la Quinta (3/2) o nota Sol. Dos consonancias perfectas.
Además el 6 en medio del 4 y el 9 plantea una doble relación 3/2 o Quintas dobles.(24)
– octaedro 8C+6V =12A+2 y el cubo 6C+8V =12A+2, reproducen los números 6/8/12 (ubicados en la siguiente etapa de la Lambda) que indican una relación 12/6 (2/1) de Octava, 8/6 (4/3) de Cuarta y 12/8 (3/2) de Quinta. Tres consonancias perfectas que también reproduce el cubo variando las relaciones entre vértices y caras.
Podemos continuar el crecimiento de Lambda hasta la sexta potencia 26 y 36 y vemos cómo ese interior de la Lamda sigue rellenándose por unos números que deben resultar ya familiares en las descripciones de los poliedros de L.Pacioli: 8/12/18/24/36/48/72/96, etc. Así, 12/8, 36/24, 72/48… representan los números de la línea 8-27 o tercera potencia; los siguientes a la cuarta potencia, y los últimos a la quinta potencia de los números 2 y 3.
– cuboctaedro 14C+12V= 24A+2, dichos números corresponden ya a las siguientes etapas de la multiplicación. Las 14 caras distinguen dos tipos de polígonos: 6 cuadradas y 8 triangulares; luego los números 6/8/12/24 corresponden a una Cuarta (8/6), una Quinta (12/8) y dos Octavas (24/12 y 48/24). Cuatro consonancias que también reproduce el dodecaedro rómbico, de nuevo variando las relaciones entre vértices y caras.
– el rombicuboctaedro: 26C+24V= 48A+2. De nuevo, las 26 caras corresponden a 8 triangulares y 18 cuadradas. Así los números se ordenan como 8/18/24/48 o como una Quinta doble (18/8), una Cuarta (24/18) y una Octava (48/24)… De nuevo, cuatro consonancias perfectas. F37
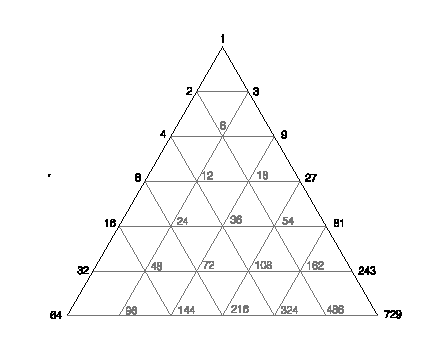
Y si consideramos el número de ángulos que estos poliedros contienen veremos que llegamos a la sexta línea (96/72) del “creced y multiplicaos” en consonancias perfectas.
Y en este pequeño repaso, podemos ver que el rombicuboctaedro es el más “esférico” de todos los considerados. (Curiosamente, en los plintos del ábside de Poblet, se combinan las esferas y los rombicuboctaedros).

Retomando el hilo de los poliedros, decíamos que Fuller al llegar al rombicuboctaedro se para en ese proceso. Nosotros podríamos seguir mencionando que el rombicuboctaedro tiene también su dual. Se conoce como icositetraedro deltoidal formado por 26 vértices, 24 caras y 60 aristas. Esto es, cumple la ley de Euler donde ambos intercambian los números de vértices y caras manteniendo la igualdad de aristas. F38.
– Rombicuboctaedro 24V+26C= 48A+2
– Icositetraedro deltoidal 26V+24C= 48A+2

F38. Icositetraedro deltoidal.
Imagen https://es.wikipedia.org
y por ello, dos nuevos polígonos duales. Con lo cual en el proceso hemos añadido un nuevo poliedro que pertenece a los sólidos de Catalán.
Estos poliedros, en número de 13, son conocidos por ser los duales de los sólidos arquimedianos. Surgen de la unión de los puntos medios de las caras de dichos sólidos y por ello, sus caras ya no son polígonos regulares pero sí todas las caras son iguales. Esto es:
– los poliedros Platónicos son regulares y todas sus caras son polígonos regulares e iguales (en nuestro caso, el cubo caras cuadradas y el octaedro triángulos equiláteros)
– Los poliedros Arquimedianos son semirregulares y combinan dos tipos de caras de polígonos regulares (en nuestro caso, cuboctaedro y rombicuboctaedro con caras cuadradas y triángulos equiláteros)
– En los poliedros de Catalán, sus caras ya no son polígonos regulares pero sí todas las caras son iguales (en nuestro caso, en el dodecaedro rómbico todas las caras son rombos).
Pero en este proceso hay algo que no acaba de ajustarse…
Antes hemos escrito que al biseccionar las aristas del cuboctaedro, surge el rombicuboctaedro …pero no parece ser cierto del todo. No podemos truncar un sólido con dos tipos de caras o formas poligonales regulares y terminar con caras que sean polígonos regulares del nuevo poliedro.
Y así parece que existen 2 tipos de rombicuboctaedro nombrados indistintamente como rombicuboctaedro menor y el pseudorombicuboctaedro, son como hermanos mellizos.
El Rombicuboctaedro pequeño o menor resulta de truncar hasta la mitad las aristas de un cuboctaedro pero el resultado es que las caras son casi cuadradas, pequeños rectángulos.
Paulo Porta (25) describe que la manera correcta es truncar los vértices de un cubo, no de un cuboctaedro, hasta el 58,58% (2-√2) de las aristas; el siguiente paso es, al sólido resultante, truncar las pequeñas aristas hasta el punto medio de las aristas de las caras cuadradas. También es conocido como Ortobicúpula cuadrada elongada. F39
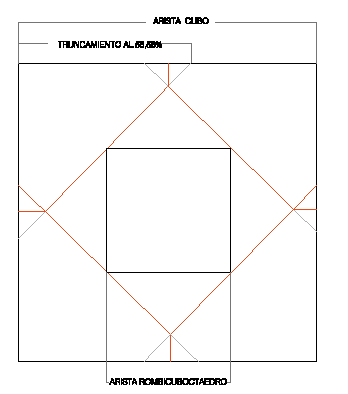
Luego parece ser que para llegar al rombicuboctaedro, el proceso por truncamiento no es tan directo desde el cuboctaedro y desde el cubo… Sus características ya las hemos mencionado: 26 caras (=18 cuadrados y 8 triángulos), 48 aristas y 24 vértices. F40
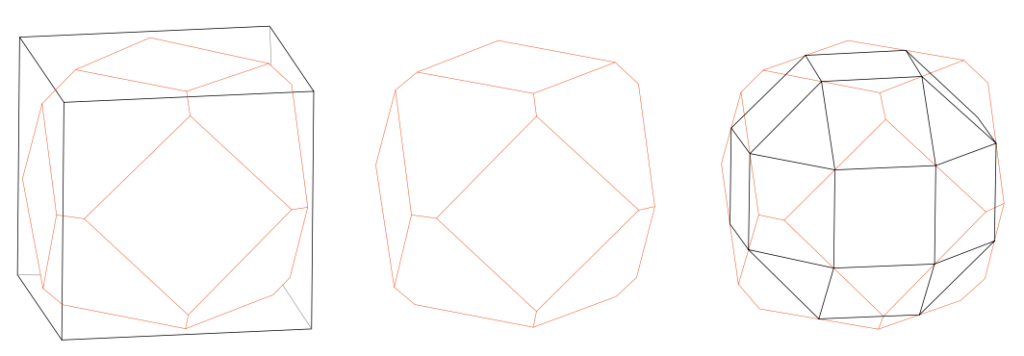
El mismo Paulo Porta cuenta que el Pseudorombicuboctaedro deriva del rombicuboctaedro pequeño al que se puede rotar 45º una cúpula de 5 cuadrados y 4 triángulos; este poliedro pierde los planos de simetría que pasan por el eje de giro pero no la igualdad de ángulos. También conocido como Girobicúpula cuadrada elongada, está compuesto de las mismas 26 caras (=18 cuadrados y 8 triángulos), 48 aristas y 24 vértices. F41 y F 42
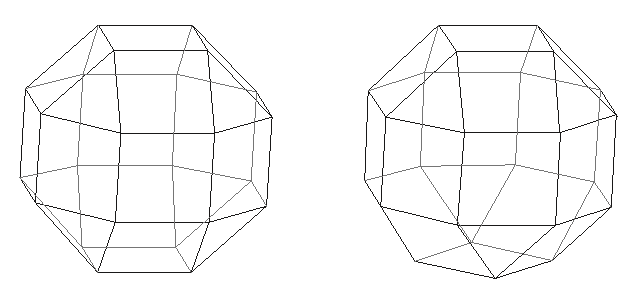
F42. Pseudorombicuboctaedro.
Sí hay que aclarar que el poliedro mencionado de la F41, corresponde al Rombicuboctaedro del texto de Luca Pacioli.

Hay otra manera de llegar a este poliedro de forma más directa y en continuidad con los procesos ya descritos. Fijémosnos con más detalle en el dodecaedro rómbico o rombododecaedro.
Sabemos ya que es:
– Poliedro dual del cuboctaedro que ya hemos descrito en páginas anteriores compuestode 12 caras iguales.
– El truncamiento del cubo y del octaedro a mitad de sus aristas produce el cuboctaedro.
– La estelación de ambos poliedros conduce al dodecaedro rómbico.
Esto es, entre el cuboctaedro y su dual, el dodecaedro rómbico, tenemos al cubo y al octaedro. F43 y F44.

¡Curioso poliedro dual! Así, como el cubo o hexaedro se apila ordenadamente para rellenar el espacio, la pareja tetraedro/octaedro tiene también esa capacidad de llenar el espacio. Pero no la tiene ni el icosaedro ni el dodecaedro pero sí el dodecaedro rómbico. (26) Fuller define las geometrías más importantes de la experiencia espacial en estos cinco poliedros: tetraedro, octaedro, cubo, equilibrio vectorial o cubooctaedro y dodecaedro rómbico. (27)
Además, hemos empezado a ver la importancia que Fuller dedica al dodecaedro rómbico. Desde la Sección 426.00 hasta la 430.00 del libro “Synergetics”, va enumerando las múltiples e importantes características con un lenguaje complejo, difícil de seguir.(28) Pero lo que sí queda claro en su lectura es la importancia del dicho poliedro como la forma más económica de llenar (junto a la matriz vectorial isotrópica) y subdividir el espacio. También este poliedro representa el mayor volumen con la menor superficie de todas las formas geométricas que macizan el espacio.
Este proceso de generación del rombicuboctaedro mediante el dodecaedro rómbico es fácil seguirlo comenzando desde su desarrollo plano.
La F45 muestra el desarrollo plano del poliedro y las caras cuadradas dibujadas del futuro rombicuboctaedro. Esta operación es matemáticamente sencilla y dibujada en la F46, la cara rómbica de este poliedro está formada por la diagonal menor a la que la damos el valor unidad y la diagonal mayor toma el valor de √2.

F46. Geometría de la cara rómbica.
La inserción de la cara cuadrada en el rombo significa que el lado del cuadrado del rombicuboctaedro toma el valor de (2-√2) o el valor 58,58% del valor unidad. Este valor ya ha de resultar conocido pues corresponde al valor del truncamiento de la arista del cubo para llegar, en dos pasos ya recorridos anteriormente, al cuboctaedro en las F39 y F40.
En la F47, se colorean los triángulos a truncar o mejor dicho, los futuros tetraedros a truncar y en la F48, se colorean además las pirámides cuadradas.


Por último en las F49, 50 y 51, podemos ver el montaje espacial de los anteriores desarrollos planos con especial hincapié en la F50 donde los tetraedros y las pirámides de cuatro caras están preparadas para truncar.

F51. Rombicuboctaedro resultante.
Así, según este proceso y distancias de truncamiento el poliedro resultante es el rombicuboc-taedro y que cumple lo que ya antes comentamos de que no se puede truncar un sólido con dos tipos de caras o formas poligonales regulares y terminar con caras que sean polígonos regulares del nuevo poliedro.

Recapitulemos:
Comenzamos este camino con esa singularidad en la iglesia del monasterio de Poblet: la labra de un poliedro arquimediano, un rombicuboctaedro, en el plinto de la columna del ábside de la iglesia construido en el siglo XII. No ¡uno¡, sino varios situados junto a esferas. Dato mencionado en el libro sobre la traza de la iglesia donde ya apuntábamos un posible acercamiento al tema (1). ¿Qué sentido podían tener esas figuras allí situadas?…
La investigación sobre temas afines condujo a Richard Buckminster Fuller, el arquitecto que más aportó al conocimiento de los poliedros en el siglo XX planteando una nueva visión muy unida al estudio de las características de nuestro espacio tiempo.
El estudio de sus investigaciones nos condujo a plantear este trabajo desde el principio: recorrer las nociones básicas de los poliedros regulares y sus características, paso a paso; también las operaciones geométricas más sencillas cuyo resultados son en parte origen de los poliedros arquimedianos.
Y en el camino, llegamos a ese particular poliedro arquimediano, el cuboctaedro o “equilibrio vectorial” como representación de vectores de energía, todos ellos iguales en fuerza y donde cualquier diferencia de presión, carga, spin, etc, conduce al campo fuera del equilibrio; a la importancia de ese instante donde surgen las diferencias, donde nacen las relaciones y emergen todas las formas poliédricas, en palabras del propio Fuller.
Asistimos a esa capacidad de transformación de unos en otros y sus relaciones; conocimos al dodecaedro rómbico, pareja del cuboctaedro, esa dualidad innata entre los poliedros y llegamos al rombicuboctaedro.
Con esas tres etapas recorridas, y con la naturalidad que da la familiaridad con ellos, revisamos la investigación realizada sobre las armonías utilizadas en las trazas de los edificios de los siglos XII y XIII del monasterio; también el libro “La Divina Proporción” en dos distintas ediciones. Releímos las descripciones de Luca Pacioli y observamos los dibujos de Leonardo da Vinci… Empezamos a reconocer la importancia que, en el Renacimiento, le daban alrombicuboctaedro, similar en su tratamiento a los poliedros regulares y al cuboctaedro.
Un paso más atrás, de nuevo al siglo XII y “reconocer” el ambiente cultural en el que se movía el conocimiento: la Escuela de Chartres y la orden del Císter, y en común el pensamiento de San Agustín. (Recordemos que Poblet es de los primeros monasterios cisterciense de la península). Necesaria y obligadamente retrocedimos a Platón y su diálogo «Timeo» como origen de esa línea de conocimiento en el tiempo. El dodecaedro rómbico, dual del cuboctaedro, empezó a llamar la atención…
Datos del pasado y del presente se fueron ordenando y empezaron a surgir los primeros resultados en la investigación sobre el posible origen del rombicuboctaedro, Revisamos las distintas operaciones geométricas de truncamiento y estelación de poliedros, los dos o tres diferentes sistemas de llegar al mismo poliedro y sobretodo, la curiosa situación de tres poliedros con algunas variaciones en la posición de las caras y con similar nombre (rombicuboctaedro menor, mayor y pseudo).
Estudiamos su desarrollo en el plano y sus relaciones espaciales con el cubo, el cuboctaedro y el dodecaedro rómbico y vimos que con éste último, la relación era sencilla y directa: la inserción geométrica de la única cara cuadrada posible en la cara rómbica del dodecaedro rómbico daba origen a nuestro rombicuboctaedro.
El proceso de la investigación ha quedado descrito; queda en último término, la comprensión de la continuidad de ese poliedro a lo largo del tiempo.
Tal vez, en los siglos XII y siguientes, el conocimiento y diferente entendimiento del concepto espaciotiempo, haya hecho que nuestro rombicuboctaedro sea la mejor representación “cristalizada” de la esfera como poliedro.
– Hemos señalado ese relación simbólica en el plano, entre el círculo como representación del Cielo y el cuadrado su representante en la Tierra; en el espacio, la esfera y el cubo y entre ellos, el tercer elemento, el rombicuboctaedro (recordemos lo que decía Pacioli: que el rombi-cuboctaedro proviene del cubo). La esfera como la infinitud de puntos equidistantes del origeno centro y su primera “materialización”, nuestro poliedro.
– Hemos recordado la definición de Platón de la Proporción: “Es imposible combinar dos cosas sin la existencia de una tercera. Es preciso un vínculo que las una. No ha y mejor vínculo que el que hace de sí mismo y de las cosas que une un todo único y eterno”. ( El rombicuboctaedro como vínculo y armonía entre la esfera y el cubo).
– Hemos visto que los 48 vértices o vórtices del rombicuboctaedro mantienen su equidistancia al centro y las 24 aristas o vectores representando las fuerzas y tensiones del poliedro, comienzan a diferenciar, como caras, los dos primeros polígonos regulares, triángulo y cuadrado, en número de 8 y 18.
– También que la relación entre vértices y aristas: 48/24= (2/1), es una relación de Octava; la relación entre los dos tipos de caras 18/8= (9/4)= (3/2)(3/2), es una consonancia de Quinta duplicada.
– Hemos analizado la Lambda Platónica, donde los números 8/18 y 24/48 van rellenando el interior de la Lambda. Es el “creced y multiplicaos en consonancias perfectas”.
Y todo esto es cierto. Lo cumplen los números, vértices, caras y aristas del rombicuboctaedro.
Tal vez, llegados al siglo XXI, podamos decir que la pareja cuboctaedro/dodecaedro rómbico represente esa continua y constante “inter-transformabilidad” e “intercomplementaridad” (en términos de Fuller); esa dualidad o doble aspecto continuamente cambiante de nuestra realidad en la comprensión de este nuestro espaciotiempo.
Recordemos, como hemos dicho al principio, que el espacio no es esa nada vacía que permite cualquier configuración…
Las investigaciones de Fuller en el siglo XX, sobre el empaquetamiento de esferas tangentes como un sistema de llenar el espacio sin vacíos ni huecos, un llenado completo, era una forma de comprender el espacio mismo; un medio a través del cual las restricciones o características de ese mismo espacio podían tomar forma visible mediante los poliedros y la esfera como unidad de comienzo, como repetía: “omnisimétrica” en la realidad espacial, le permitió llegar a dos opciones válidas para “llenar el espacio”. En la segunda opción o empaquetamiento cúbico, alternando tetraedros como forma ”llena” y octaedros” como forma “vacía” del espacio, (29) hizo su aparición como corazón del sistema, el cuboctaedro. Y siguiendo sus palabras, podemos decir que:
– Doce esferas alrededor de una, creando ángulos de 60º radial y axialmente con tetraedros y octaedros alternados, resulta ser el empaquetamiento más útil en estas características de este espaciotiempo.
Pero no sólo eso. Siguió afirmando la importancia del cuboctaedro, o equlibrio vectorial, o matriz de vectores isótrópicos, como la red de energía cósmica subyacente, origen de los procesos energéticos. También, afirmó la importancia de su dual, el dodecaedro rómbico, renombrado como “esférico” (30), definido como “corazón del equilibrio vectorial” (31) y descrito como la forma más económica de llenar el espacio.
Y todo esto también es cierto.
Resulta que nos hemos encontrado que el dodecaedro rómbico o “esférico” es el origen más sencillo de nuestro rombicuboctaedro representado en los plintos del ábside de la iglesia del monasterio cisterciense de Poblet. Posiblemente, el “hijo” del siglo XII, ocupó el lugar del “padre” del siglo XX, ese lugar que Fuller afirma con el comentario: “el primer sintonizador de radio debe haber sido un dodecaedro rómbico”. (32)
Curiosa palabra “sintonizador” …
Puede ser que la pareja “cuboctaedro/rombododecaedro” cumpla esta función de la geometría (recordemos su anterior definición como ciencia de las configuraciones y estudio de las relaciones) sintonizando energía y forma; como cuboctaedro o equilibrio vectorial, matriz de todos los patrones y origen conceptual de todos los sistemas energéticos; como dodecaedro rómbico o esférico, forma más económica de llenar el espacio y la más perfecta representación del mayor volumen con la menor superficie de todas las formas geométricas que “empaquetan” el espacio.
Esta pareja singular se ha desvelado como un origen del rombicuboctaedro y sus funciones han quedado planteadas en una nueva etapa, tal vez, de mayor comprensión y conocimiento del espacio-tiempo que habitamos.

Volvamos al siglo XII. El maestro de obra Anoll ha replanteado el ábside de la iglesia partiendo del cuadrado central del transepto. Un juego de semicírculos concéntricos expandiéndose según determinadas consonancias. F52
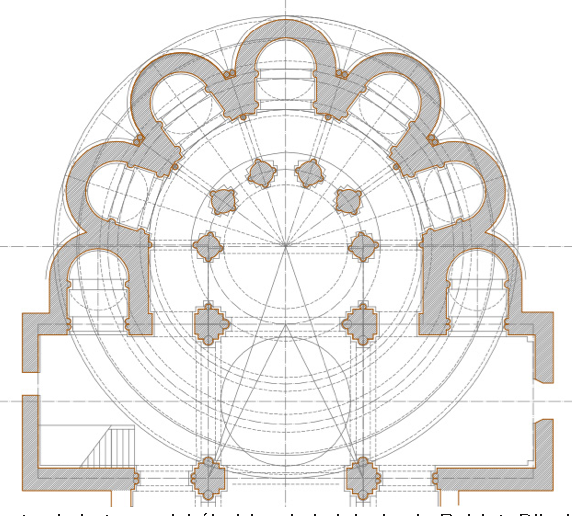
Ha de resolver geométricamente el juego de fuerzas y tensiones de los 6 arcos formeros de la semicúpula del ábside y del muro vertical de cerramiento que la sostiene: un semicírculo de 6 pilares cilíndricos atados entre sí por arcos apuntados. Pilares con cuatro baquetones adosados situados en los ejes radiales para apoyo y entronque de los arcos radiales de las bóvedas del deambulatorio: bóvedas de crucería trapezoidales. Y cohesionando el conjunto, las siete capillas radiales diferenciando en posición las dos del transepto, definiendo así la cabecera de la iglesia como unidad arquitectónica.
Anoll sabe de la geometría angular de la planta de 180º en 5 sectores de 36º, de los vectores o líneas de esfuerzos que se conjugan en cada vértice o vórtice construido en piedra. Puras relaciones geométricas de tensión estructural, en este caso, complejas…
Estudia cada punto de apoyo con el mismo rigor geométrico que implícitamente ordena las fuerzas: la columna como un círculo que se inscribe en su base cuadrada, los cuatro baquetones adosados como cuatro semicírculos igualmente apoyados en sus basas cuadradas, situados en los ejes radiales de la planta del ábside… F53
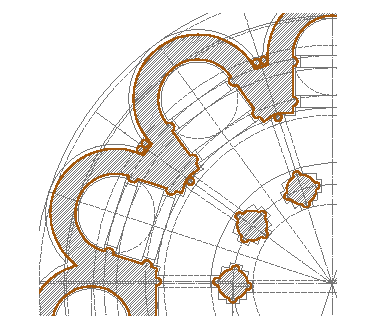
Comprende el simbolismo del círculo y del cuadrado… también que el elemento intermedio entre ambos, el vínculo entre ambas representaciones en el plano es otro polígono, el octógono, símbolo del elemento Aire. Es el mismo proceso para la geometría del espacio definida en tres niveles: la planta cuadrada en la tierra, la planta octogonal intermedia en el aire y el círculo como origen y apoyo de la cúpula como envolvente y cubrición en el cielo.
Se eleva del plano y pasa al espacio, recuerda que el vínculo entre la esfera y el cubo, es un nuevo poliedro…
Contempla esas esquinas triangulares planas, vacías entre los zócalos cuadrados y las basas de los fustes de las columnas…Toma un pequeño bloque de piedra. Comienza la labra “achaflanando las cuatro aristas”(33) del bloque cúbico convirtiéndolas en ocho caras o planos iguales. Ese primer movimiento radial y simétrico desde el centro, en definitiva esférico, define la dimensión de la arista del nuevo poliedro; su perímetro de ocho aristas iguales conforma un octógono inscrito en la planta y, “despuntando los vértices”,(33) el mismo polígono define las dos secciones verticales ortogonales de la piedra cúbica. Octógono regular como límite exterior formal, del rombicuboctaedro. F54.

F55. Detalle de un rombicuboctaedro en la columna del ábside.
Maria Luisa Lopez Sardá
Primavera- Verano 2024
– Todas las maquetas han sido realizadas por Jose Carlos Velasco.
– Todos los dibujos han sido realizados por la autora.
– Todas las fotografías y planos del Monasterios de Poblet corresponden al archivo de documentación del libro: “Anoll: primer arquitecto de Poblet”.
NOTAS:
1. Todo la investigación realizada se publicó en el libro, «Anoll: primer arquitecto de Poblet«. Autores: José Luis Bozal y Maria Luisa Lopez Sardá. Editorial Pirineo. 2021
2 y 3. «A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller«. Amy C. Edmonson. Design Science Collection Series. Editor Arthur L. Loeb. Department of Visual and Enviromental Studies. Harvard University.
8. «A Fuller Explanation…» Nos apoyaremos en la descripción que Amy C Edmonson desarrolla en el mencionado libro.
9. La variación en el porcentaje de truncado puede variar desde 1 para el triángulo, √2 para el cuadrado, Φ para el pentágono y 2 para el truncado completo entendiendo el valor 2 la mitad de la arista.
10. «Equilibrio vectorial: es el punto cero de partida de los sucesos o de los no-sucesos, es el teatro vacio y el circo vacio y Universo vacío, preparado para albergar cualquier acto y cualquier público».
La sección 430.00 Vector Equilibrium”… común denominador del tetraedro, octaedro y cubo..” hasta la 456.00, del libro Synergetics 1, Fuller los dedica a ir desgranando todas las características del cuboctaedro.
11. Synergetics: Sección 240.55: Shape is exclusively angular. 240.56: Shape is independent of size. 515.14:…Angles are constant and independent of size. Size is always special case experience… etc.
12. La representación en planta de las esferas que circunscriben a cada tetraedro forma en planta, la conocida Flor de la Vida.
13. A partir de la sección 456.00 o la transformación del equilibrio Vectorial en su fase icosaédrica, Fuller se centra en el Jitterbug o las contracciones simétricas del cuboctaedro. La Fig.460.08 del libro Synergetics, plantea las etapas que finalizan en primer lugar en el octaedro y en fase posterior, en el tetraedro. Se adjunta imagen del libro.
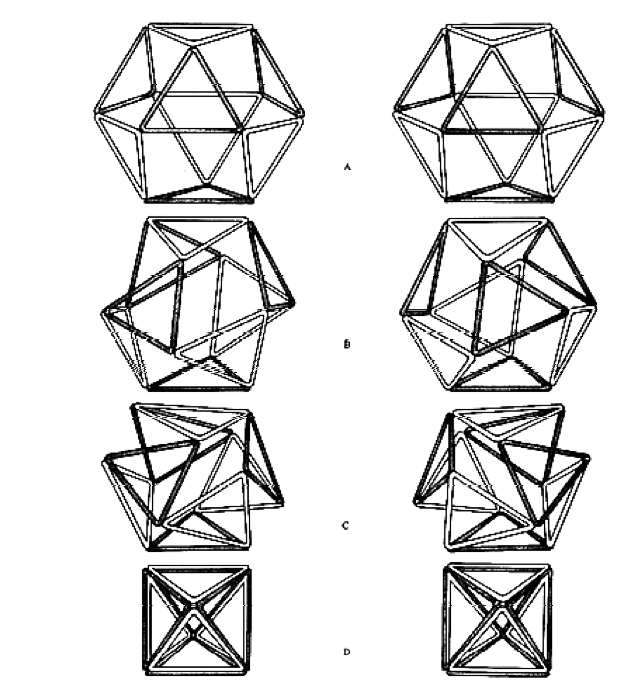
14. los proyectos de Rwgray. Enciclpedia de poliedros. www.rwgrayproyects.com.
15. Jitterbug es movimiento rápido que supone un desplazamiento lineal y un giro angular sobre su mismo centro. Descrito con claridad y detalle en el libro «A Fuller Explanation: “… el jitterbug es una transformación continua a través de innumerables etapas de transición, tanto regulares como no, y en ciertos intervalos emerge un poliedro ordenado…”
16. Synergetics: Sección 240.03: Unity is complex and at minimum two.
17. «Acordes Arquitectónicos: otra geometría de la proporción y la armonía en arquitectura«. Maria Lujsa Lopez Sardá.. Editorial Fisuras. 2014
18. «La Divina Proporción«. Luca Pacioli. Editorial Akal con prólogo de Antonio Gonzalez.
19. En la impresión de «La Divina Proporción» de Ed. Losada con prólogo de Aldo Mieli, se cita una nota a pié de página que parece ser del propio Mieli, para explicar ese otro proceso que planteábamos en el libro sobre Poblet de expansión mediante simetría esférica. “Esto es, despuntando los vértices y achaflanando sus aristas”.
20. «La catedral gótica«. Cap.2. Otto Von Simson. Alianza Forma. 1982.
21.Hay un precedente en el libro «Armonía en el trazado geométrico de Santa Maria de Veruela«. Ed. Electa.1996 de la misma autora dedicado al análisis completo del monasterio cisterciense de Veruela, en la provincia de Zaragoza, cuya carta de fundación por Ramón Berenguer IV, es anterior en unos pocos años al de la fundación del monasterio de Poblet. La investigación continuó con la medición de las iglesias cistercienses de Moreruela y Fitero, posteriores a Poblet y Veruela, y los estudios de sus trazas se incorporaron como tercera parte del libro ya mencionado «Anoll: primer arquitecto de Poblet«, titulado El legado de Anoll.
22. www.acordesarquitectonicos.com. Artículos: Proporción 1: Las Medias Proporcionales. ML.Lopez Sardá.
23. «240.64 Synergetics. En un sistema estructural
- el nº de vértices (cruces) es: siempre divisible por 2.
- el nº de caras (aperturas) es siempre divisible por 4.
- el nº de aristas (trayectorias) es siempre divisible por 6.«
24. En la web antes mencionada, sección de Artículos, hay uno dedicado a «La Octava y la vivencia del tiempo«. Recordar las relaciones básicas de la gama diatónica. 1/1 Unisono o Primera, 9/8 Segunda o Re, 5/4 Tercera o Mi, 4/3 Cuarta o Fa, 3/2 Quinta o Sol, 5/3 Sexta o La y 15/8 Séptima o nota Si y 2/1 u Octava.
25. www.pauloporta.com poliedros
26. «Synergetics: 536.43. Synergetics. the most complete description of the domain of a point is not a vector equilibrium but the rhombic dodecahedron, because it would have to be all space filling and because it has the most omnidirectional symmetry. The nearest thing you could get to a sphere in relation to a point, and which fill all space, is the rhombic dodecahedron.«
27. «Synergetics: 201.03.Synergetics makes possible a rational, whole number, low-integer quantation of all the important geometries of experience because the tetrahedron, the octahedron, the rhombic dodecahedron, the cube and the vector equilibrium embrace and comprise all the lattices of all atoms.«
28. «Synergetics: 426.22. The rhombic dodecahedron´s 12 diamonds faces are the unique planes always occurring perpendiculary to the midpoints of all vectors radii of all closet-packed spheres whenever and whenever they may be metaphysically or phisically regenerated, ie. perpendicular to the midpoints of all vectors of all isotropic vector matrixing».
29. Amy Edmonson en su libro ya citado, relata en el Capítulo 8 las dos opciones de empaquetamiento centrándose en el proceso de Fuller de considerar una esfera y su entorno inmediato. La primera opción llamada “hexagonal” delinea la forma de un poliedro y la segunda, llamada empaquetamiento “cúbico” fue considerada por Fuller la más simétrica.
30. «Synergetics: 426.31. A spheric is any one of the rhombic dodecahedra, the center of each of whose 12 diamonds facets is exactly tangent to the surface of each sphere formed equidistantly around each vertex of the isotrpic vector matrix.«
31. «Synergetics: 955.50. Rhombic Dodecahedron at heart of Vector Equilibrium. Nature is always start every ever freshly with the equilibrious isotropic-vector matrix field. Energy is not lost; it is just not yet realized. It can be realized only disequilibriously. 955.51. Al the heart of the vector equilibrium is the ball in the center of the rhombic dodecahedron».
32. «Synergetics: 426.42. The fact that the rhombic dodecahedron can have its 144 modules oriented as either introvert-extrovert or as three-way circunferencial provides its validity between broadcasting-transceiving and noninterference relaying. The first radio tunning crystal must have been a rhombic dodecahedron.«
33. Hace referencia a la nota 19 del libro «La Divina Proporción» editado por Losada.
Dejar un comentario