
Este artículo comienza en Vicenza cuando fuimos a visitar el Museo Palladio en el Centro Internazionale di Studi di Architettura Andrea Palladio (CISA) situado en el palacio Barbarano en Vicenza.
En la segunda sala hay una maqueta con un patrón constructivo de la columna palladiana. Su altura es de cuatro hiladas y cada hilada esta compuesta por siete piezas iguales de forma triangular y de material plástico a excepción en la última hilada donde una de las piezas triangulares es de ladrillo cerámico. Esto es, la geometría del círculo de la planta es un heptágono regular.
No vimos otra maqueta con otra posible división; de ello, parece deducirse que esta era la forma de construcción en planta de las columnas palladianas y eso resultaba poco habitual…

Si recordamos conceptos básicos de geometría, la división del círculo en partes iguales entre los ocho primeros números naturales 3, 4, 5, 6, 8, 9 y 10 da siempre un número entero de grados radiales y cada división define y nombra a los siete primeros polígonos regulares: 120º para el triángulo, 90ª para el cuadrado, 72º para el pentágono, 60º para el hexágono, etc. La construcción con escuadra y compas de estos siete primeros polígonos regulares forma parte del conocimiento elemental de geometría.
La excepción es la división por 7 que da un ángulo radial de 51,412857…º .
Es decir, hay siete posibilidades de dividir el círculo en partes iguales con ángulos enteros …En pleno Renacimiento, ¿por qué entonces utilizar esta división del círculo en 7 dado que siempre será una construcción aproximada realizada con escuadra y compás?
Me vino el recuerdo de la lectura del libro de Keith Critchlow “Time Stands Still. New Light on Megalithic Science” (1).
En uno de los capítulos dedicado al Número como Cualidad, habla del posible comienzo de las matemáticas aplicadas en los logros de los trenzados, tejidos y anudados de las primeras culturas neolíticas y menciona la cuerda de 12 intervalos y 13 nudos como principal instrumento de la ciencia constructiva del neolítico.
Una cuerda trenzada de una longitud de 12 unidades, dividida secuencialmente con nudos, de manera que haya incrementos idénticos entre ellos, es la mínima medida que puede ser triangulada en un patrón 3/4/5 para dar un ángulo recto perfecto.
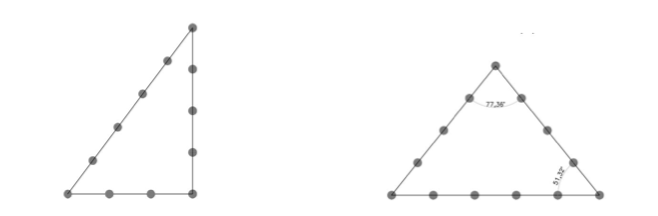
Esta descripción responde a la cuerda 3/4/5 compuesta de 12 espacios y 13 nudos, conocida como escuadra egipciaca y/o pitagórica, cuyo uso, como herramienta de medida, siguió siendo habitual por los maestros de obra en la construcción de las catedrales medievales. Fig.4
El mismo autor también menciona otra cuerda utilizada en la cultura neolítica. Es la compuesta de 13 espacios y 14 nudos, triangulada como la escuadra 4/5/4 o triángulo isósceles de base 5 y lados 4. Es una escuadra curiosa pues ninguno de sus tres ángulos es un número entero. Fig.5
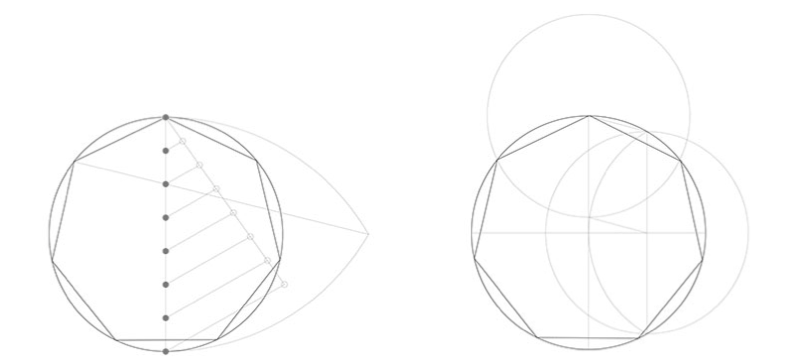
Lo interesante es que si tomamos esta cuerda, así triangulada en 4/5/4, fijando dos vértices de ella, dos de los lados definen un ángulo radial casi igual al de la construcción del heptágono con un error del 0,1%… Fig.6
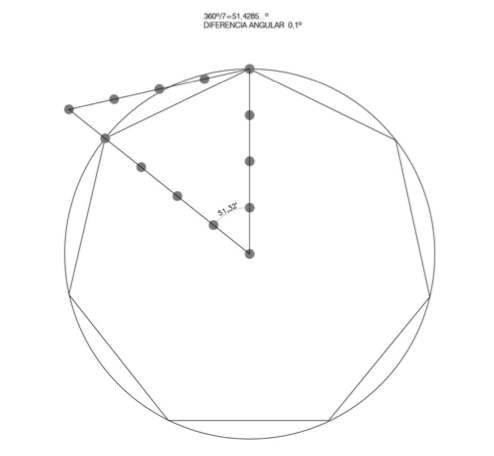
Hacemos notar que este sistema de construcción del heptágono no necesita del límite de la circunferencia circunscrita para trazarlo; basta sólo fijar un vértice como centro y un lado de cuatro intervalos como dirección de construcción y triangular la cuerda de 13 intervalos en 4/5/4.
Según Critchlow, esta cuerda tuvo menos consideración en la cultura cristiana al estar asociada al calendario lunar (13 lunas en un solo año) y podemos añadir, al ser el 13 un nº primo divisible sólo por sí mismo, mientras que la cuerda de 12 espacios estaba asociada al calendario solar, además de su correspondencia con los doce signos del zodiaco y con el sistema duodecimal y también contener un máximo nº de divisores.
Si con esta cuerda formamos una circunferencia obtenemos un círculo dividido en 13 partes iguales que permite formar una estrella de 13 puntas. Polígono de 13 lados cuyo ángulo radial, 27,692..º vuelve a no ser un número entero. Fig.7
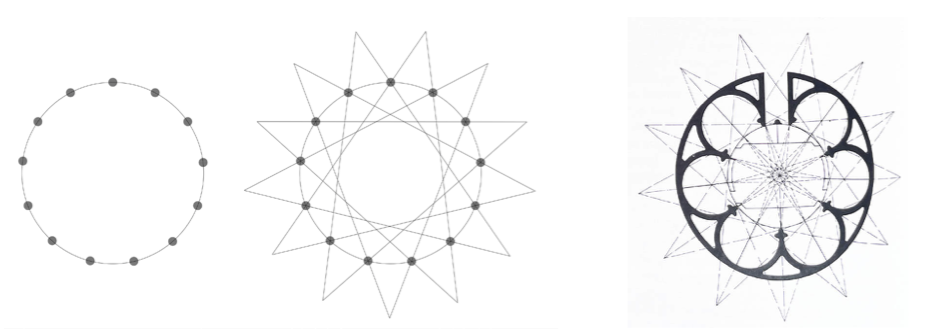
Fig.8 El laberinto de la catedral de Chartres muestra en su centro la estrella de 13 puntas. Dibujo del libro Time Stand Still.
Y comenta que este dibujo, es la base del laberinto de la catedral de Chartres. El simbolismo asociado a ello puede derivar del calendario lunar, opción posible al estar el templo dedicado a la Virgen o también al derivar el nº 13 como suma de los doce signos del zodiaco junto con el sol. Fig.8
Como dato curioso, podemos añadir que la siguiente cuerda de 30 intervalos y 31 nudos cuya triangulación produce un ángulo recto está asociada con los números 12/5/13. Fácil de recordar si es de uso común las dos cuerdas anteriores de 12 y 13 intervalos.
Cuerda como materialización del compás cuando fijamos un punto y el otro moviéndose en su rededor a distancia constante. Pero también cuerda como unidad de medida definida por sus intervalos anudados. La Aritmética y la Geometría como una misma disciplina unidas en el instrumento de cuerda.
De todo ello, podemos deducir que esta utilización del heptágono como división constructiva de la planta en triangulaciones iguales de la columna palladiana, pueda tener su origen en el uso de la cuerda de 13 intervalos en la construcción siguiendo la tradición medieval.
Y añadir que Palladio, y posiblemente todo el Renacimiento, utilizase el Número y la Medida no sólo para la proporción y armonía de los espacios sino también como una herramienta de trabajo aplicable a todos los elementos del proyecto y de la construcción y como sucede con el ejemplo que hemos expuesto, hasta a los detalles constructivos de la obra. Una forma de “saber” que impregnó toda una forma de “hacer” remontándose muy atrás en el tiempo.
María Luisa López Sardá
Septiembre 2022
Notas a pie de artículo:
- (1) Keith Critchlow. Time Stand Still. Floris Book. 1979
Dejar un comentario